La Commission de réflexion sur l’Enseignement des Mathématiques, menée par J.-P. Kahane en 2002 (in Fénichel et al., 2004), dégage quatre enjeux pour l’enseignement de la géométrie :
– permettre aux élèves de s’approprier une vision de l’espace,
– amener les élèves à un apprentissage du raisonnement (observation et construction de figures géométriques),
– diffuser les aspects culturels et artistiques de la géométrie,
– donner des outils géométriques utilisables dans la vie courante.
Tout au long de l’école primaire, l’élève doit être amené à passer de l’espace sensible, physique (se déplacer, déplacer, se repérer, dessiner, fabriquer) aux représentations géométriques (décrire, repérer, identifier, nommer) pour accéder aux concepts (démontrer, prouver).
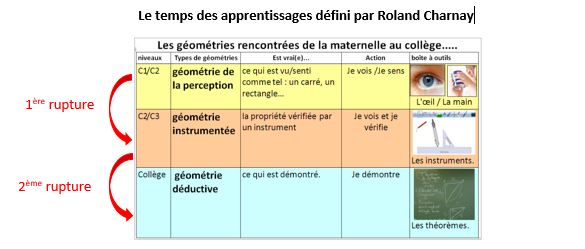
Ces ruptures correspondent à des étapes dans l’acquisition de connaissances géométriques.
Pour accompagner au mieux ces ruptures, il existe 2 leviers fondamentaux :
- La manipulation avec la volonté de faire évoluer les rapports aux figures chez les élèves
- Le langage
Ces deux axes ont été étudiés dans la situation dite du Pliox (situation de reproduction de figures par pliage) par l’enseignante chercheuse de l’INSPE Aix-Marseille, Claire Guille-Biel. (Actes du séminaire national de l’ARDM – 19 mars 2016)
- 1 – Faire évoluer le rapport aux figures à l’école élémentaire
Raymond Duval, professeur émérite de Mathématiques, définit comme figure à l’école élémentaire une représentation d’une figure géométrique dont les propriétés se traduisent par des propriétés visuelles contrôlables avec des instruments. A ce titre, Marie-Jeanne Perrin, enseignante chercheuse à l’INSPE de Lille, ajoute que cette figure peut être obtenue par un assemblage de formes par juxtaposition ou superposition.
La situation PLIOX porte sur les deux premiers niveaux d’appréhension d’une figure :
- L’appréhension perceptive porte sur des objets figuraux 2D, voire 1D (notamment par la mise en évidence du réseau de droites visible sur le verso du PLIOX) ;
- L’appréhension opératoire : partage des figures internes colorés en sous-figures (décomposition et reconfiguration), modification positionnelle induite par le coloriage mais aussi par l’endroit du Pliox (au tableau)
La situation PLIOX met en jeu des connaissances spatiales au sens de Berthelot et Salin (1999-2000) dans le micro-espace 3D. Ces connaissances sont liées à l’orientation et à la position des différentes figures dans les modèles.
Cette situation est bien un problème géométrique. Il s’agit dans un premier temps de reconnaitre différentes figures géométriques (polygones particuliers), d’en reconnaitre les propriétés et de mettre en évidence des relations entre elles.
- 2 – Le langage
L’étude de cette situation Pliox dans les classes conclut à une évolution dans l’acquisition du vocabulaire géométrique par les élèves au cours de la séquence et montre l’existence d’une corrélation entre l’usage du lexique géométrique par l’enseignant et celui des élèves mais d’autres facteurs entrent en jeu comme le contrat didactique mis en place par l’enseignant et le déroulement de l’activité.

Au-delà de l’acquisition du vocabulaire, le langage et les autres signifiants (représentations géométriques) participent à la construction du sens du concept. Ils ont aussi une double fonction de communication et de représentation selon les champs conceptuels de Vergnaud.
