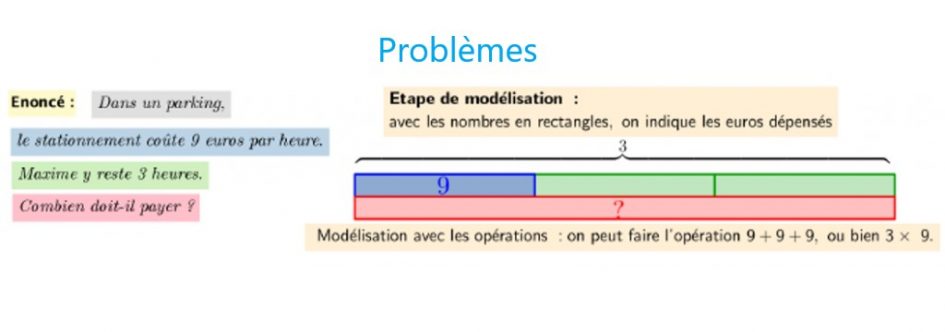
Conformément aux programmes, la représentation iconique est un des enjeux de l’apprentissage de la résolution de problèmes arithmétiques. Il en existe plusieurs. Les représentations, sous forme de schémas bien adaptés, permettent la modélisation des problèmes proposés. Elles sont systématiquement utilisées lors des résolutions de problèmes menées face à la classe, afin de servir de référence aux élèves. C’est pourquoi, le modèle utilisé doit être transposable, comme un langage commun, dont on peut garder une trace. C’est une représentation particulière qui fait partie des représentations possibles. BO n°3 du 26 avril 2018
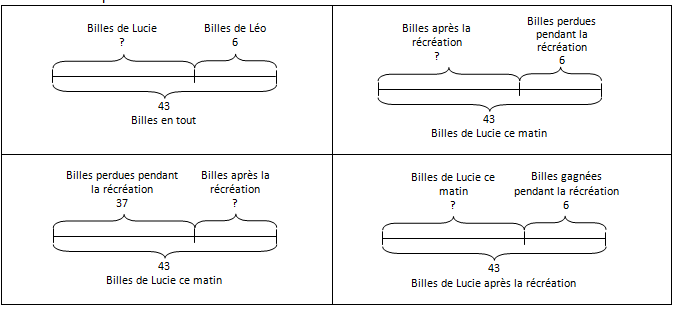
La schématisation dite « en barre » est très utilisée dans les pays anglo-saxons et en Asie car elle s’inscrit dans la construction du nombre et permet notamment de mieux concevoir la relation entre nombre et longueur.

Elle permet d’unifier les modélisations et de simplifier les représentations en restant proche du sens du contexte et proche des nombres et permet avec adaptation de représenter la structure décimale, de visualiser les opérations et les techniques de calcul…
Avantages :
- Proche des longueurs représentées sur la droite graduée
- Utilisation possible de deux dimensions du rectangle
- Symétrie des données intuitives
- Lien avec les opérations explicites
- Lien fort avec les fractions d’unité
Point de vigilance :
Pas de soustractions possibles : nécessité de comprendre la soustraction comme complément par superposition de longueurs.
Comment construire les schémas en barre ?
- Cas des problèmes additifs : modèle « partie-tout »
Rôle de l’unité : Les parties et le tout ne sont pas des nombres mais des grandeurs associées qui sont représentées : elles doivent être explicitées.
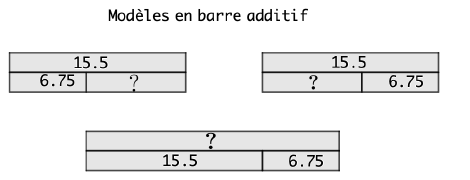
Tous les problèmes additifs basiques peuvent se représenter de cette manière : bien préciser au préalable la quantité la plus grande de celles qu’on étudie.
Les opérations correspondantes sont des additions ou des additions à trou : la soustraction découlera de cette dernière formulation, pouvant être comprise comme complément ou comme retrait.
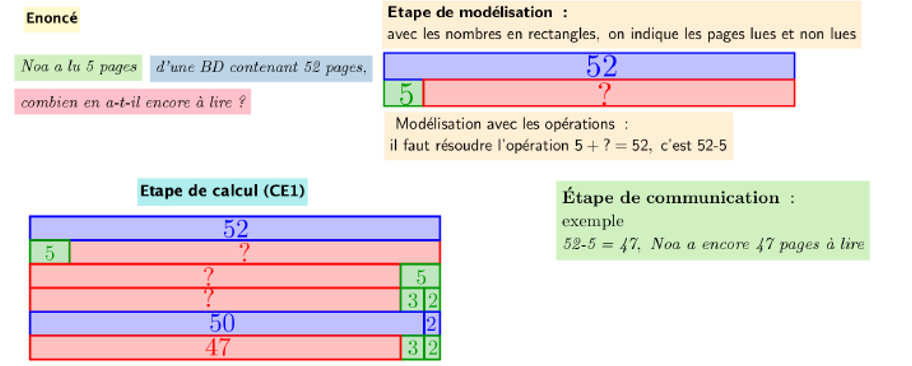
- Cas des problèmes multiplicatifs : un schéma compatible avec le modèle additif
Rôle de l’unité : indispensable à préciser, en particulier pour des problèmes impliquant des fractions.
Un seul schéma pour toutes les opérations.
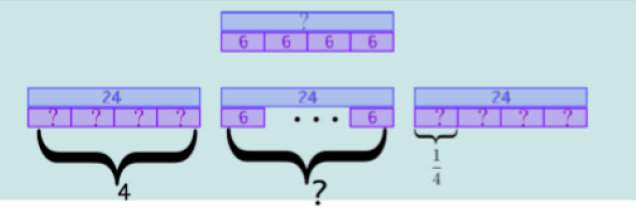
Les opérations correspondantes sont des multiplications ou des multiplications à trou : la division découlera de cette dernière formulation, pouvant être comprise comme partage, comme quotition, comme division euclidienne avec reste. Bien réfléchir aux légendes accompagnant le schéma pour qu’il soit clair et non surchargé.