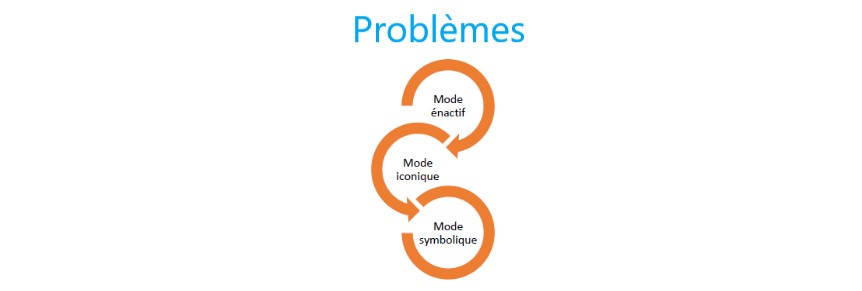
Il existe trois registres de représentation selon Bruner 1973 et Barth 1987 :
– le mode énactif: on agit
– le mode iconique: on représente
– le mode symbolique: on abstrait
Les représentations évoluent avec l’âge, pour passer du mode concret manipulatoire au mode iconique puis abstrait. A l’école primaire, l’élève doit évoluer dans ses représentations mentales, graphiques, conceptuelles afin de pouvoir mobiliser des modèles. Mais, comme le préconise Mélanie Guenais, formatrice Référent Maths de Circonscrition, faire un schéma et l’ériger en modèle mathématique, ça s’apprend !
- L’apprentissage du modèle en barre de manière explicite.
M. Lappara et C. Margolinas expliquent la nécessité d’enseigner méthodiquement chacune des schématisations pour construire des savoirs, et cela particulièrement lors du cycle 2, dit « des apprentissages fondamentaux ». Pour cela, il apparaît primordial de partir de la représentation des élèves et ce, depuis le cycle 1.
Le schéma: un écrit de savoir? Marceline Laparra, Claire Margolinas, 2009)
La modélisation en barre s’appuie sur ces représentations.

Le schéma ne doit pas être qu’une trace écrite mais bien la transition de la manipulation vers la modélisation algébrique. Pour se faire, il doit être explicité. Le recours aux réglettes Cuisenaire, tout comme les cubes empilables sont des outils appropriés. Il permet aussi de faire le lien avec la droite graduée.

2. Les enjeux de l’utilisation du modèle en barre
- Les modélisations en barres renforcent les compétences sur le sens des opérations et leurs propriétés d’une part, sur le calcul et la structure décimale d’autre part.
– Pour permettre de comprendre le sens de la construction du nombre par accumulation d’unités, en se référant à la longueur des rectangles qui les représentent,
– Pour permettre de faire les liens entre écriture décimale et décomposition selon les unités de numération.
- Elles peuvent servir d’appui pour les calculs, en particulier pour les calculs impliquant des fractions lorsque les faits arithmétiques sur la fraction quotient ou opérateur ne sont pas encore institutionnalisés.
- Elles peuvent également servir d’appui pour communiquer un raisonnement lorsque l’écrit ou même l’oral font défaut.
- Elles permettent aussi de résoudre des problèmes complexes et présentent l’avantage de se libérer des données de l’énoncé et allègent ainsi la charge cognitive.
- Elles sont aussi un moyen de différencier. Exemple : un carré peut représenter une unité – en lien avec les cubes (niveau débutant); un rectangle représente une quantité (niveau expert).
- Elles se révèlent enfin être des modèles pré-algébriques au cycle 3
Exemple d’énoncé de l’enquête CEDRE 2015 :

La modélisation attendue pour un élève de fin de cycle 4 est la modélisation algébrique vue au collège. Les modèles en barre, plus concrets, permettent une transition souple vers cette modélisation algébrique.
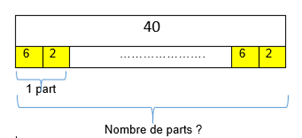
Au cycle 4, ce même problème pourra être résolu ainsi :
Soit x le nombre de magazine ou de livre acheté.
2x + 6x = 40 soit 8x = 40 soit x = 5