A la veille d’organiser la semaine de maths qui aura lieu du 7 au 14 mars 2022 sur le thème « maths en forme(s) », il nous semble intéressant de vous proposer la situation du napperon élaborée par Marie-Lise Pelletier Grand N n°68. En effet, au-delà de l’apprentissage de la symétrie axiale, elle permet véritablement de travailler le cheminement mathématique : anticipation, manipulation, analyse de l’erreur et validation
Une situation enrôlante
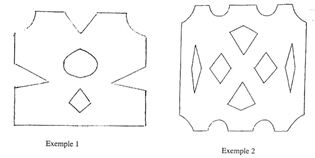
Les élèves doivent reproduire un napperon qui est affiché au tableau (cf. exemples ci-dessous). Pour cela, ils doivent effectuer tous les pliages qu’ils jugent nécessaires, puis, sans déplier, faire tous les découpages qu’ils considèrent utiles. Une fois fini, ils déplient et comparent leurs réalisations avec le modèle.
S’il y a conformité, ils ont relevé le défi de reproduction. Si cela n’est pas conforme, les élèves conservent leur réalisation, sans la froisser, sans la jeter, pour pouvoir l’étudier et recommencer avec un autre papier.
Les critères de réussite sont précisés.
Un napperon sera considéré comme conforme au modèle si :
- même nombre de formes
- même découpe
- même position relative
- même orientation
Lors du dépliage, les élèves peuvent être très surpris des résultats obtenus car leur napperon est souvent extrêmement différent du modèle.
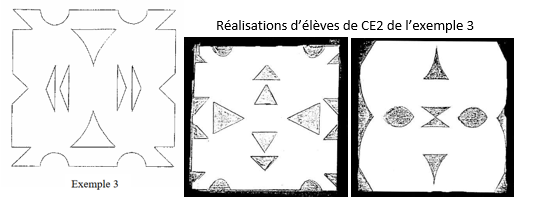
La validation se fait individuellement (ou en binôme) par confrontation au modèle en s’appuyant sur les critères définis. Les élèves n’ont généralement pas trop de difficultés à effectuer cette comparaison.
Les modèles doivent permettre aux enfants de valider seuls leur réussite ou de repérer leurs erreurs. Pour cela, il est important de choisir des napperons avec des découpes de formes différentes et en nombre différent sur chacun des axes et sur deux côtés consécutifs du carré.
De multiples variables
Cette situation enrôlante peut être adaptée pour tous niveaux de classe.
En effet, l’enseignant peut jouer sur :
- le nombre d’axes de symétrie
- le nombre de découpes
- la forme des figures
- la forme du napperon
Différentes procédures avec prise en compte de l’erreur
Comme il est rarissime que les élèves parviennent au bon résultat dès le premier essai, la prise en compte des essais erronés est fondamentale pour :
- mener une réflexion et une analyse fine des effets d’un découpage sur une feuille pliée en 2, en 4, ou en 6.
- émettre des hypothèses sur les modifications à effectuer pour obtenir le résultat souhaité
- mettre en évidence les axes de symétrie du napperon
Les procédures sont les suivantes :
– identification du nombre d’axes de symétrie et réalisation des pliages associés, repérage des éléments de découpe en prenant en compte les positions relatives (procédure experte)
– pliage en deux quel que soit Ie nombre d’axes de symétrie et reproduction des découpes sur ce pliage en deux,
– pliage en deux ou en quatre puis reproduction par découpage sur le papier ainsi plié de toutes les découpes du modèle complet,
– pliage en deux ou en quatre, découpages de certaines parties, dépliage et rectification sur la feuille dépliée.

La richesse de la mise en commun
Elle poursuit un double objectif : définir les méthodes et les notions en fonction du niveau de la classe.
En s’appuyant sur les échecs, puis les évolutions, elle est l’occasion de répondre au problème de reproduction posé en amenant les élèves à verbaliser leurs connaissances des figures usuelles.
Ce temps doit s’attacher à leur permettre d’utiliser un vocabulaire spécifique et de justifier leur point de vue grâce aux relations et aux propriétés géométriques : alignement, perpendicularité, parallélisme, égalité de longueurs, symétrie axiale, etc…
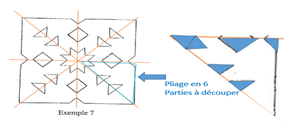
Dans cet exemple, la méthode consiste à repérer tous les axes de symétrie pour effectuer les pliages et les découpes associées. Elle permet d’aborder les propriétés des figures planes et particulièrement les usuelles (triangle isocèle, carré, losange) par le prisme de leurs axes de symétrie.
En conclusion, le problème du napperon permet une réelle dévolution de l’élève dans l’activité mathématique, qui, à partir de contraintes (pliage, découpage), mobilise des savoirs géométriques. Il doit servir de référence pour la symétrie axiale.
