Nous avons choisi pour ce dernier numéro de l’année scolaire 2021-2022 de vous présenter 2 puzzles géométriques qui ont comme origine le carré à travers le prisme des grandeurs et mesures : le tangram et Curvica. En effet, leur étude du cycle 1 au cycle 3 peut véritablement influer sur les représentations des élèves notamment pour les notions de longueurs et d’aires.
- Le tangram
C’est un puzzle chinois dont l’origine exacte est incertaine. Selon une légende, il serait né de la maladresse d’un empereur chinois : il aurait fait tomber un carreau de céramique qui se serait brisé en 7 morceaux. Cherchant alors à le reconstituer, il créa des milliers de figures.
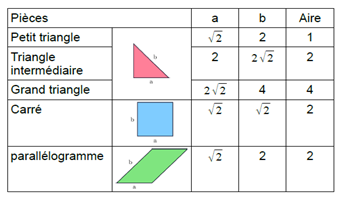
Le tangram est donc composé de sept polygones réguliers : 5 triangles isocèles (2 grands, 1 moyen, 2 petits), un carré et un parallélogramme. A l’inverse d’un puzzle classique, les pièces sont monochromes (on ne peut pas s’appuyer sur un dessin, une image à reproduire) et les côtés sont tous droits.
Le principe du jeu est qu’une figure doit toujours être constituée des sept polygones. Les pièces ne peuvent être que juxtaposées et non superposées.
Nous avons déjà proposé une utilisation du tangram en géométrie avec la présentation de la mallette Maman.
Dans le cadre d’un enseignement en grandeurs et mesures, il est intéressant pour l’enseignant d’avoir en tête toutes les égalités de longueurs et d’aires de ce jeu.
Aussi, si on choisit l’aire du plus petit triangle comme égal à une unité d’aire (prise comme unité de longueur au carré), la longueur des petits côtés du petit triangle est donc égale à √2 (unité de longueur (a). L’hypoténuse (b) de celui-ci vaut 2.[1]
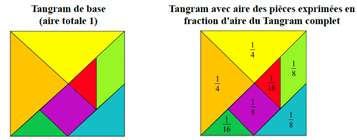
Dès le cycle 1, après une découverte en jeu libre, puis une étude descriptive des pièces, on peut travailler sur les égalités de longueurs avec un jeu de domino des longueurs notamment (cf. vu en classe cycle 1). La réalisation de multiples figures d’abord par superposition (figures apparentes) puis moins dirigée au cycle 2 avec les mêmes pièces ancre l’idée que des pièces de même taille (d’une même aire) peuvent former différentes figures.
Au cycle 3, on peut réinvestir les compétences en écriture fractionnaire pour les calculs d’aires mais aussi travailler la distinction entre aire et périmètre.
2. Curvica
Le jeu Curvica est un puzzle pédagogique de 24 pièces qui a été inventé par Jean Fromentin (créateur de la rubrique Jeu à l’APMEP) en 1982. Son objectif est avant tout d’amener les élèves à comprendre de manière ludique les notions d’aires et de périmètres par comparaison sans introduire de calcul ni de formule. Ces deux notions sont liées car elles sont relatives à une forme et pourtant elles sont indépendantes et il n’y a pas lieu de les confondre.
Il s’appuie sur l’un des invariants de base de la géométrie euclidienne : le plus court chemin pour aller d’un point à un autre est la ligne droite. L’arc de cercle entrant ou sortant pour arriver à ces deux points est forcément plus long. En effet, le principe de Curvica (d’où l’appellation) est de partir d’un carré et de décliner des carrés incurvés avec des côtés concaves ou convexes dont la longueur est identique. Ils sont superposables.
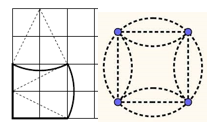
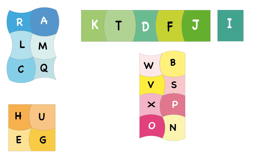
Les 24 pièces sont nommées par des lettres pour faciliter la communication des échanges mais aussi pour éviter que les pièces soient retournées.
Dans un article de l’Irem de la Réunion très complet sur Curvica, Yves Martin fait le classement suivant des différentes pièces :
• 6 pièces sans aucun segment (totalement courbes), 18 avec segment(s)
• 5 pièces (hors carré) ayant deux côtés parallèles
• le carré I
• 4 pièces ayant un seul angle droit (elles forment, ensemble, un carré).
• 8 pièces ayant un seul côté qui est un segment.
Le tri et la comparaison des périmètres de différentes pièces amènent à lever certaines résistances insoupçonnées.
En effet, Jean Fromentin, dans l‘article APMEP Curvica, constate que si beaucoup d’élèves disent volontiers que le périmètre d’une pièce est la longueur du tour complet de la pièce, à savoir la somme des longueurs des quatre côtés, il reste difficile pour eux d’admettre une égalité de périmètre entre les pièces A et Q par exemple.
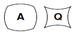
Faire tourner les pièces l’une contre l’autre en faisant un tour complet permet de conclure que les côtés convexes (sortants, à l’extérieur) ou concaves (entrants, à l’intérieur) sont de même longueur.
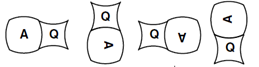
Le tri et la comparaison des aires qui interviennent ensuite montrent une stratégie bien différente, ce qui renforce la séparation des deux notions et leur donne du sens. Il s’agit alors mentalement de se référer au carré de base pièce I (car pour certaines lettres telles que le N, la superposition ne fonctionne pas) et de savoir si on enlève ou si on ajoute de la surface.

En cherchant ensuite des formes de même périmètre et même aire, on assoit définitivement les deux concepts tout en ayant prouvé qu’il n’y a pas de corrélation entre eux.
Si cette ressource a été créée pour les cycles 3 et 4, l’étude des pièces du puzzle pour les cycles 1 et 2 ainsi que la réalisation du puzzle ne manque pas d’enjeu pédagogique tels que la taille, la symétrie, la recherche des angles droits, la différence entre les lignes courbes et les lignes droites.
[1] https://unige.ch 5ème semaine des mathématiques 2013
