Les concepts d’aire et de périmètre posent problème à la majorité des élèves arrivant au collège, et cela perdure pour beaucoup d’entre eux jusqu’en troisième, voire au-delà.
- Les difficultés liées au concept
- L’aire et le périmètre sont amalgamés à la surface et liés à sa forme.
Les élèves ont une perception de la figure qui englobe différentes caractéristiques : sa forme, son encombrement, son contour, son intérieur. S’il est facile de rattacher la notion de périmètre à la longueur du contour, l’aire ne se distingue pas clairement de l’objet qu’est la surface. Une diminution de l’aire est ainsi comprise comme une diminution de la surface, avec sa forme, et va de pair avec une diminution de périmètre.
Périmètre et aire sont deux notions différentes attachées à un même objet, ce qui incite à considérer que ces deux grandeurs varient de la même manière : à périmètres égaux, aires égales ; classement identique des figures suivant l’aire et le périmètre…

La figure de gauche est perçue comme un grand carré amputé d’un petit carré, alors que celle de droite est perçue comme un grand carré augmenté d’un petit : ce qui est exact en terme de décomposition et recomposition. Ce qui est erroné, c’est le mouvement de pensée qui traduit cette perception en opération (soustraction ou addition) sur les deux grandeurs périmètre et aire. Car il est vrai qu’à l’addition perceptive des deux formes correspond l’addition des aires mais il n’en est pas de même au niveau des périmètres.
L’identification trop précoce entre grandeurs et nombres favorise l’amalgame entre aires et périmètres.
- L’aptitude à décomposer l’aire d’une surface comme somme ou différence des aires de figures simples qui la composent n’est pas opérante (par exemple l’aire d’un trapèze rectangle comme somme ou différence des aires d’un rectangle et d’un triangle rectangle).
- Les difficultés liées à l’unité légale : l’unité d’aire (le cm2 par exemple) est définie en référence à un carré. On retrouve la surface avec sa forme et la longueur. Cette définition constitue incontestablement un obstacle.
Ces erreurs trouvent probablement leur origine dans des confusions s’appuyant sur des perceptions erronées. Intuitivement, nous avons tendance à penser (souvent inconsciemment) que si nous augmentons une surface, le nouveau périmètre augmente aussi (et réciproquement). Une construction insuffisante de la grandeur est aussi responsable d’un certain nombre de ces difficultés.
2- L’acquisition d’un concept
Tout apprentissage doit commencer par un travail de dissociation des concepts. Le recours trop rapide à des démarches faisant appel aux mesures risque de ne pas favoriser ce travail. Il est donc souhaitable, de recourir à des procédures de comparaison qui ne fassent pas appel à la mesure.
Ce qui suppose d’explorer des situations où :
– à périmètre constant les aires vont varier (et dans quelles limites),
– à aire constante, les périmètres vont varier (et dans quelles limites)
– le périmètre et l’aire vont varier dans le même sens (ce qui n’est pas surprenant) mais aussi en sens contraire (ce qui est moins conforme à l’intuition).
L’activité Curvica peut permettre à certains élèves de mieux s’approprier chacune des deux notions du fait que cette activité les fait fonctionner de concert. Curvica permet de comparer sans calcul des périmètres et des aires de dessins construits à partir d’un carré, et amène les élèves à prendre conscience que ces deux grandeurs sont indépendantes.
Dans un premier temps, les situations d’apprentissages s’articulent surtout autour de « manipulations réelles » (inclusion, superposition, découpage et recollement, ….). Elles permettent, entre autres, de dissocier les notions d’aire et de longueur, en particulier aires et périmètres sans l’intervention des nombres.
L’acquisition « d’images mentales » (découpage et superposition fictifs d’une surface, etc…) à partir de ces situations permettra aux élèves d’imaginer plus tard des procédures pour résoudre des problèmes et par ce biais, d’entrer dans « l’action » mathématique.
On peut caractériser l’acquisition d’un concept par le schéma suivant (d’après « apprentissage géométrique au cycle 3 et argumentation en géométrie ». Actes du XXVIIe colloque inter IREM) : un exemple avec l’aire.
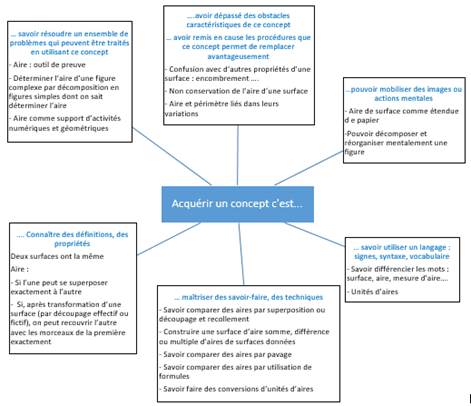
3. Des activités de reproduction : les puzzles géométriques ou puzzles à juxtaposition comme le tangram ou Curvica
Dès la maternelle, les activités menées autour de puzzles géométriques permettent aux enfants de se familiariser avec des formes géométriques simples. Ils apprennent à les identifier par l’analyse informelle de leurs caractéristiques et s’habituent à observer ces formes dans des positions diverses.
Les enfants approchent la forme géométrique en tant qu’élément faisant partie d’un tout et construisent l’idée qu’un tout peut être constitué d’éléments différents.
Progressivement, ils sont amenés à prendre conscience de l’équivalence de surfaces obtenues par différents assemblages de formes. Ils commencent ainsi à se forger de manière ludique les premières images mentales qui leur permettront de construire peu à peu la notion de la conservation de l’aire par découpages et assemblages.