Au cycle 2, il est attendu que l’élève sache lire et écrire un nombre et connaisse la valeur des chiffres en fonction de leur position. Il doit savoir utiliser des écritures en unités de numération (5d 6u, mais aussi 4d 16u ou 6u 5d pour 56). Ces tâches de codage / décodage relèvent d’apprentissages complexes et les résultats des évaluations nationales (CP, CE1, 6ème) montrent encore à quel point les acquisitions restent fragiles pour bon nombre d’élèves.
Le Chiffroscope est un jeu au service d’une meilleure connaissance de la numération décimale de position.
- La complexité de la numération décimale de position pour les élèves
La numération de position est un procédé d’écriture des nombres, dans lequel chaque position d’un chiffre est reliée à la position voisine par un multiplicateur, qui est nommé « base du système de numération ». On parle de numération décimale de position car elle est en base 10.
A ce titre, elle diffère, par exemple, de la numération romaine qui n’est pas un système de numération positionnel, mais un système additif dans lequel chaque symbole a une valeur fixe.
Il s’agit donc pour les élèves d’assimiler un double aspect du système de numération décimale de position:
- L’aspect de position : chaque chiffre désigne une unité de numération selon sa position dans le nombre;
- L’aspect décimal : chaque nombre peut être décomposé en unités, dizaines, centaines ou toute autre unité de numération. Selon le chercheur Frédérick Tempier, construire l’aspect décimal de la numération amène les élèves à utiliser les différentes unités de numération selon différents points de vue. http://numerationdecimale.free.fr/
Lire, écrire un nombre n’est donc pas une simple activité de codage/ décodage, mais bien une activité complexe qui inclut la composition / décomposition du nombre.
L’équipe du LéA CiMéLyon (Soury-Lavergne, Croquelois, Martinez, Rabatel) en s’appuyant sur les travaux de didacticiens (Vergnaud 1990 ; Balacheff & Margolinas, 2005), s’est particulièrement intéressée à caractériser ce que savent faire les élèves. En effet, même quand les élèves se trompent, ils ont des conceptions du système de numération décimal. Mieux comprendre leurs conceptions permet ainsi de créer des situations et des étayages appropriés.
Ils ont distingué six invariants opératoires dans les stratégies des élèves.
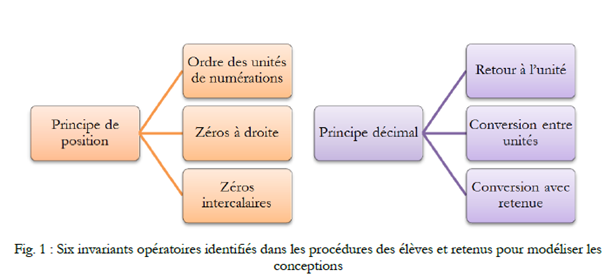
Comme l’ont constaté Houdement et Tempier (2019), la conception décimale fait encore défaut à une grande partie des élèves, qui mobilisent essentiellement le principe de position. Ils utilisent uniquement le retour à l’unité dans leur conception décimale. Cela génère des difficultés quand ils rencontrent les grands nombres, les nombres décimaux et les grandeurs.
2. Le chiffroscope au service du principe de position et des conversions entre unités
Le Chiffroscope tend à mobiliser au moins quatre invariants opératoires : ceux du principe de position et la conversion entre unités.
Pour se faire, il s’appuie sur une approche libre du tableau de numération, l’érigeant comme outil de l’apprentissage de la numération décimale.
L’absence d’un tableau de numération figé, fermé permet de ne pas limiter l’élève dans la réalisation du problème de numération « lire/écrire le nombre ». Le fait de tirer des cartes a plusieurs chiffres ou plusieurs cartes pour une même unité de numération va déstabiliser l’élève qui ne pourra alors pas opérer avec l’ordre des unités de numération. En revanche, comme les unités de numération sont clairement explicites, le nombre peut parfaitement être déterminé. Le retour à l’unité peut vite apparaitre couteux même infructueux dans le cas des décimaux. Les élèves vont progressivement s’appuyer sur le tableau comme outil pour convertir et pas uniquement pour positionner correctement les cartes.
Le fait d’écrire les nombres dans le tableau et hors du tableau est primordial pour réaliser que ce qui est possible dans le tableau ne l’est plus en dehors. Par exemple, dans le tableau de numération, on peut indiquer 23 dans la colonne des unités de mille et cela signifie sans ambiguïté 23 unités de mille. Mais en dehors du tableau, pour signifier les 23 unités de mille, il faut écrire obligatoirement 23 000. C’est-à-dire positionner le 2 immédiatement à gauche du 3 pour signifier les dizaines de mille et des zéros pour les centaines, dizaines et unités.

Pour tous les élèves, il est intéressant de ne pas réduire la taille du tableau aux nombres connus. Un tableau qui contient plus de colonnes que nécessaires aide les élèves à considérer le tableau comme un outil en n’utilisant que ce dont ils ont besoin. A l’inverse, s’il manque des colonnes, les élèves le complètent en fonction de leurs besoins en l’agrandissant à gauche ou à droite tout en s’appuyant sur l’ordre des unités de numération.
Ce tableau est dit « flottant » c’est-à-dire sans indication des unités de numération : ainsi une colonne n’est pas dédiée à une unité de numération a priori. Les unités de numération ont un ordre fixe, il s’agit donc de le respecter à partir de la première unité de numération positionnée dans le tableau. Il est important de souligner que la dernière colonne de droite n’est pas nécessairement celle des unités simples (les élèves seront alors plus à même de comprendre les décimaux), en revanche respecter l’ordre des unités de numération est obligatoire.
L’objectif ici est bien d’amener les élèves à travailler le principe décimal et à comprendre le lien entre écriture chiffrée du nombre et valeur représentée.
Les conclusions du LéA CiMéLyon (Soury-Lavergne, Croquelois, Martinez, Rabatel) ont montré que l’utilisation du Chiffroscope permet de faire évoluer les conceptions des élèves.
Il semblerait intéressant, comme le propose F. Tempier, de réinvestir les compétences acquises à travers des résolutions de problèmes propres à la numération. En effet, les résistances y sont encore coriaces.

