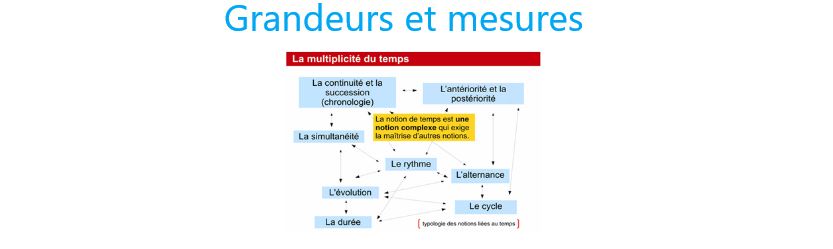
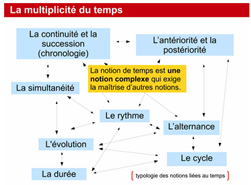
Le concept de temps est complexe et englobe une multitude de notions à maitriser. Parmi elles, la durée est difficile à appréhender, notamment pour les plus jeunes, car elle dépend non seulement du développement de l’enfant en lui-même mais aussi de l’apport de son expérience individuelle sur le temps. De plus, la notion de durée s’enchevêtre avec d’autres notions telles que la simultanéité ou encore la chronologie.
- Des difficultés liées à la perception
- La première difficulté de la notion de durée est la composante subjective du temps qui fait que chacun appréhende la notion de durée différemment selon son vécu et son expérience. « Dix ou quinze minutes passées à attendre quelqu’un qui n’arrive pas sont perçues comme beaucoup plus longues que quinze minutes de récréation! ». Le temps objectif et mesurable passe toujours à la même vitesse alors que le temps subjectif semble passer plus ou moins vite selon la situation.
- La durée, grandeur fortement liée à la perception, est aussi une grandeur qui n’est pas palpable : les durées se rapportent davantage à des évènements qu’à des objets : il est donc difficile de la percevoir de façon isolée (objet instable).
2. Des confusions entre la durée « temps-mesure » (durée) et le repérage chronologique « temps-repère » (horaire/date)
- Le temps est d’abord perçu comme linéaire : écoulement chronologique du temps avant d’être perçu comme cyclique (alternance jour/nuit, semaine, années…). Cette perception première est avant tout sociale, les jeunes vivent les évènements les uns à la suite des autres.
- Le temps peut représenter à la fois :- un moment précis (ex. : 9h17, lundi 23 mars) – temps repère
L’heure : permet de se repérer dans le temps d’abord par rapport à des évènements familiers puis par rapport à des repères conventionnels et en utilisant les nombres.
- une durée (ex. : 15 minutes, une semaine, une nuit) – temps mesure.
La durée est la portion de temps qui sépare l’instant initial et l’instant final, un intervalle de temps entre deux moments. Les durées peuvent donc être additionnées et se soustraire au même titre que les longueurs.
- Les mots « heure », « demi » ou « minutes » par exemple, que prononcent les élèves en disant l’heure, n’expriment pas encore pour eux des durées, ils permettent seulement de mieux repérer la position de certains moments dans le déroulement d’une journée. A ce titre, la montre ou l’horloge est à la fois un instrument de repérage et de mesure du temps.
3. Les problèmes de conversion
• Difficulté à travailler en base 60.
• Maitrise fragile de la conversion des minutes en heures
• Difficulté à réinvestir dans des problèmes de durées
Des exemples d’erreurs fréquentes :
5h30 = 5,30 : L’élève n’utilise pas adéquatement l’écriture décimale.
Cette erreur démontre que l’élève ne comprend pas que les nombres décimaux représentent des données en base 10 (dixièmes, centièmes, millièmes, etc.) alors que le temps se calcule en base 60. Dans l’exemple, la bonne écriture décimale serait 5,5, puisque 30 minutes d’une heure (30/60) sont équivalentes à 1/2, soit 0,5. 5,30 représente 5 heures et 30 centièmes d’heure.
1h55 + 2h10 = 3h65 : problème de compréhension de la base 60.
168 minutes = 16 h et 8 min : calcul en dixièmes.
3 minutes et 120 secondes= 123 : difficulté à utiliser les différentes unités de mesure.
D’où proviennent ces difficultés ?
•L’affichage digital, le plus souvent utilisé dans la vie courante ne permet pas de travailler le fait qu’une heure est égale à soixante minutes et de mettre du sens sur ce qui est écrit sur une horloge analogique.
• Une pendule est un repère complexe pour de jeunes enfants : elle est la superposition de deux cadrans gradués différemment, celui des heures et celui des minutes. Le cadran des heures est gradué régulièrement de 1 en 1, de 1 à 12, le 12 correspondant aussi au 0. Le cadran des minutes est gradué régulièrement de 5 min en 5 min, de 5 à 60. Ces nombres-là ne figurent pas nécessairement sur le cadran de la pendule, il faut les inférer à partir des graduations des heures. Par ailleurs, les aiguilles ont des vitesses de déplacement différentes.
C’est pourquoi l’apprentissage de la lecture de l’heure s’étale du cycle 2 au cycle 3.
• La présence de 2 systèmes de numération nécessite parfois d’établir plusieurs conversions : base 60 pour les secondes et les minutes et base 12 pour les heures.
Quand on résout un problème de durées, il faut penser que 1 jour = 24 heures, soit deux fois le tour du cadran par la petite aiguille. 1 heure = 60 minutes, soit une fois le tour du cadran par la grande aiguille. 1 minute = 60 secondes, soit une fois le tour du cadran par la trotteuse.
Un appui : la ligne numérique
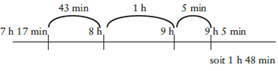
https://maths-plus.blog.ac-lyon.fr/wp-content/uploads/sites/410/2023/03/Grandeurs_et_mesures_a_l_ecole_elementaire-2.pdf pages 8 et 9
Connaître la relation entre heure et minute est un prérequis indispensable à cet apprentissage. Quand les élèves ont assimilé ces différentes relations, la connexion avec la lecture de l’heure peut être faite et les calculs de durées peuvent prendre du sens. Cela ne peut fonctionner efficacement qu’en fin de cycle 3.
Des apprentissages à construire : la durée est une grandeur mesurable qui mérite d’être construite pas à pas, mais sa construction est particulièrement délicate et semble difficile avant le cycle 3. La question des grandeurs et mesures repose sur trois étapes progressives fondamentales qui permettent de passer de la grandeur perçue à la grandeur mesurée M@ths+6.
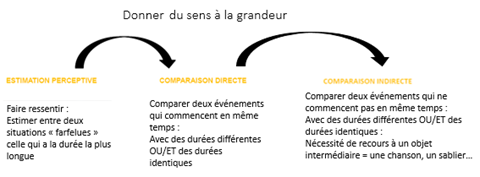
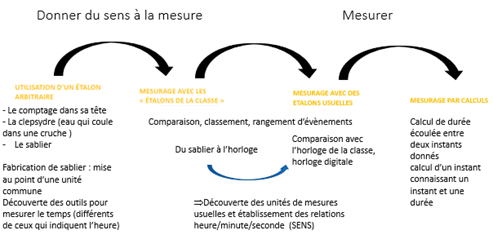
La durée d’un sablier peut aussi être utilisée comme durée de référence et permettre d’établir les premières mesures de durées.
Instrument de mesure prétexte à se confronter à des situations réelles, à manipuler, il amènera les élèves à développer des habilités de perception et de raisonnement, à mieux comprendre ce qu’est une mesure de durée et à distinguer durée et repères chronologiques.