Numicon est initialement un programme britannique d’éducation à la représentation mathématique développé depuis 1996 par R. Tacon – R. Atkinson – T. Wing. Contraction de « numeral » et « icon », cette représentation s’apparente étroitement aux « plaquettes pour l’initiation sensorielle au calcul » créées en 1923 par l’institutrice Suzanne Herbinière-Lebert et aux planchettes de l’allemande Catherine Stern développées après la seconde guerre mondiale.
https://ladigitale.dev/digiview/#/v/6516a174cbc67
En effet, les Numicons sont des plaques en plastique colorées de forme rectangulaire ou hexagonale permettant de représenter les nombres de 1 à 10, et par suite tous les suivants. Ces plaques sont trouées pour recevoir des cylindres unités et/ou les doigts. Chaque plaque représente un nombre.
Véritable outil mathématique du cycle 1 au cycle 3, les Numicons s’appuyant sur une représentation rectangulaire du nombre favorise, dès les premiers apprentissages mathématiques, une construction du nombre solide.
- Initiation au nombre « comme relation entre des quantités »
Ce qui est attendu à la fin de l’école maternelle (extrait du BO n°25 du 24/06/2021)
- Quantifier des collections jusqu’à 10 au moins, les composer et les décomposer par manipulations effectives puis mentales
- Dire combien il faut ajouter ou enlever pour obtenir des quantités ne dépassant pas 10
Les Numicons s’utilisent de manière progressive. Ils sont une des représentations du nombre parmi d’autres, les constellations de dés, les doigts, les réglettes Cuisenaire, etc…
- Discrimination intuitive : on montre des plaques et on les compare (laquelle a le plus de « trous »?)
- Correspondance terme à terme : mettre ses doigts dans les trous (avec et sans les cylindres), puis amener autant d’objets que les trous
- Travailler les différentes compositions d’un nombre
- Travail de décomposition : obtenir 5 avec plusieurs plaques
- Travail de recomposition : compléter une plaque pour obtenir un nombre
- Correspondance plaque et écriture chiffrée

En cycle 2, les Numicons sont un outil de référence pour l’apprentissage des tables d’addition, mais aussi dans la poursuite de la construction du nombre. En effet, s’interroger sur la rapidité à construire un nombre à 2 chiffres amène intuitivement les élèves à concevoir qu’il faut utiliser en priorité les plaques de 10. Ce travail peut être mené jusqu’au nombre 100.

La manipulation des Numicons permet de renforcer le sens de certains faits numériques :
- Les doubles et moitiés
- La somme de 2 nombres impairs est paire.
Enfin, en cycle 3, le travail effectué sur la construction du nombre est tout à fait transférable lors de l’apprentissage sur les fractions.
2. La représentation rectangulaire des Numicons et les propriétés arithmétiques
Elle permet de renforcer la notion de parité : la représentation des nombres en rectangle de 2 trous de large permet de se représenter mentalement la parité. Les nombres hexagonaux sont impairs.
Lors de la découverte des opérations, cette conception de « nombres rectangles » permet aussi une meilleure compréhension des priorités :
- La commutativité de l’addition et la multiplication : l’élève comprend qu’on peut changer l’ordre des termes.
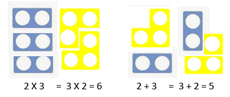
- L’associativité de l’addition et la multiplication : l’élève comprend qu’on peut regrouper les termes comme on veut.
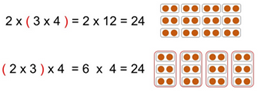
- La distributivité de la multiplication sur l’addition et la soustraction : l’élève comprend que quand on multiplie une somme de deux nombres, cela revient à multiplier chacun des termes.

Enfin, la représentation rectangulaire permet aussi de manipuler les décompositions multiples (notion de diviseurs) et la décomposition unique (notion de nombres premiers).
