Emmanuel Sander, professeur à l’Université de Genève en psychologie, a effectué de nombreux travaux de recherche en résolution de problèmes. L’orientation générale de ses recherches s’inscrit dans une perspective cognitive et développementale en lien avec les questions de l’éducation. Ses problématiques concernent la mise en évidence et l’analyse du rôle des connaissances préalables dans les activités de compréhension et de raisonnement à travers des situations d’acquisition de connaissances.
- Analogie intuitive : définition et enjeux
« L’analogie est un phénomène adaptatif fondé sur la référence au connu pour appréhender la nouveauté » (Lakoff et Johnson, 1980). Autrement dit, si on admet que toute connaissance nouvelle est appréhendée à partir de connaissances préalables, lorsqu’une notion est introduite, les analogies intuitives sont les manières dont spontanément on va l’appréhender. Face à la nouveauté, l’élève va s’appuyer sur ce qui est connu. Les analogies intuitives ont donc une valeur adaptative très importante et très pertinente puisqu’à l’école les connaissances nouvelles reposent généralement sur des connaissances préalables.[1]
Il y a de réels enjeux à s’appuyer sur les analogies intuitives et non intuitives à l’école pour orienter le développement conceptuel des élèves. En effet, il s’agit :
- d’orienter les choix de situations proposées aux élèves pour ne pas accentuer l’ancrage des conceptions intuitives,
- d’avoir conscience que les conceptions intuitives sont précoces chez les élèves, persistantes même après un enseignement (même chez l’adulte) et influentes sur les enseignants,
- d’élaborer des progressions d’apprentissage.
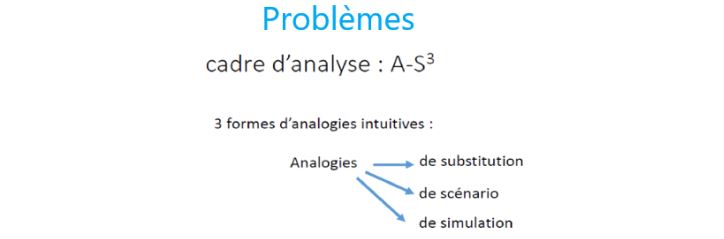
2. Trois formes d’analogies intuitives, facilitatrices ou obstructives
Les travaux de recherche d’Emmanuel Sander et de son équipe les ont conduits à concevoir un cadre théorique : le cadre A-S3. Ce cadre différencie 3 formes d’analogies intuitives qui peuvent être facilitatrices ou obstructives.

L’expérience montre qu’il y a interdépendance entre ces trois formes d’analogies mais qu’il est possible de les dissocier. Elles peuvent représenter un véritable levier au service des apprentissages.
- L’analogie de substitution (AS1)
Observons les réussites chez des élèves de CP aux problèmes suivants :

Les analogies de substitution désignent le fait que la notion mathématique est perçue par analogie avec une connaissance familière issue de la vie quotidienne. Le langage ordinaire porte en lui ces analogies de substitution. Par exemple, si on se réfère aux définitions extra-mathématiques de « soustraction » données par les dictionnaires, on trouve l’idée de « retirer », « d’enlever », « de perdre ». Or ce sens extra-mathématique ne recouvre que partiellement la notion mathématique de soustraction.Pour sortir de l’analogie de substitution, il est donc important :
- de résoudre des problèmes d’addition dans lesquels on ne gagne rien, on ne fait que perdre (ex : Paul avait des billes. Il en perd 3 pendant la récréation et maintenant il lui en reste 5. Combien de billes avait-il avant la récréation ?) ;
- de résoudre des problèmes de soustraction dans lesquels on ne perd rien, on ne fait que gagner (ex : Paul a 3 billes. Il en gagne pendant la récréation et maintenant il en a 8. Combien de billes a-t il gagnées ?) ;
- de proposer un problème dont le résultat serait plus petit dans le cas d’une multiplication (ex : 4 x 0,1 = 0,4)
- de proposer un problème dont le résultat serait plus grand dans le cas d’une division (ex : 4 ÷ 0,1 = 40)
b. Analogie de scénario (AS2)
Dans les manuels, pour 97% des problèmes à résoudre par addition, les objets additionnés appartiennent à des catégories de même niveau (ex : des pommes et des poires, ou des billes rouges et noires). 94% des problèmes demandant une division utilisent des objets reliés fonctionnellement (ex : des billes et des boites).
Pour sortir de l’analogie de scénario, proposer des énoncés de problèmes dont la relation fonctionnelle n’est pas intuitive. Exemple : J’ai 4 oranges. Si je reçois 5 pommes en échange de chaque orange. Combien aurais-je de pommes ? (dans ce problème, on échange des pommes contre des oranges au lieu de les additionner pour en faire un total de fruits).
c. Analogie de simulation (AS3)
Pour une analogie de simulation, l’intuition est liée à la possibilité d’effectuer la simulation mentale de la situation spontanément évoquée. Si la simulation est possible alors l’analogie est facilitatrice sinon c’est un facteur de difficultés.

Dans les problèmes ci-dessus, la simulation mentale « 27 pour aller à 31 » est facilitatrice (problème 1) par rapport à « 4 pour aller à 31 » (problème 3). De même, la simulation mentale « enlever 4 à 31 » (problème 4) est facilitatrice par rapport à « enlever 27 à 31 » (problème 2).
Pour sortir de l’analogie de simulation, il s’agit donc de proposer des énoncés qui ne conduisent pas mentalement à les résoudre spontanément.
3. Le recodage sémantique
Lorsque ces analogies intuitives font obstacle à la compréhension de l’énoncé, il devient nécessaire pour l’enseignant d’agir auprès de l’élève de manière à soutenir son processus de compréhension. Le recodage sémantique, par la reformulation, la verbalisation et la modélisation, vise à favoriser l’évolution de la représentation mentale initiale pour dépasser l’obstacle et mettre en œuvre la résolution. https://www.reseau-canope.fr/conseil-scientifique-de-leducation-nationale-site-officiel/groupes-de-travail/gt-5-metacognition-et-confiance-en-soi/apprendre-a-resoudre-des-problemes-le-dispositif-air2.html
Le recodage sémantique va ainsi initier une autre façon de percevoir le problème, qui, elle, est cohérente avec les objectifs mathématiques visés. Les analogies intuitives ainsi que la nécessité de passer par un recodage sémantique sont explicités dans les fiches d’accompagnement proposées pour chaque problème de la problémathèque (cf exemple ci-contre).

[1] http://centre-alain-savary.ens-lyon.fr/CAS/mathematiques-en-education-prioritaire/compte-rendus-formations-de-formateurs-mathematiques/session-2019-2020/le-role-des-analogies-intuitives-dans-la-resolution-de-problemes-arithmetiques-aux-cycles-2-et-3