L’enseignement de la droite numérique se retrouve aujourd’hui clairement énoncé dans les programmes de l’école primaire et autres documents d’accompagnement eduscol (guide CP, documents d’aide à l’analyse des évaluations, nombres et calcul au cycle 3). Elle permet de conceptualiser le nombre et est un outil pour le calcul.
- Qu’appelle-t-on « droite numérique » ?
Il existe bon nombre d’appellations : piste, fil, ligne, bande, droite, et il arrive qu’on s’y perde un peu. Or, tous ces termes font référence in fine à l’apprentissage de la droite numérique pour mieux conceptualiser le nombre.
– La piste numérique : c’est une piste de nombres. Elle permet de travailler les quantités à partir des constellations du dé, en associant cette quantité au nombre de cases avancées.

– La bande numérique : c’est le support écrit chiffré de la suite numérique. Elle est souvent composée de plusieurs lignes horizontales mettant en correspondance plusieurs représentations d’un même nombre permettant d’associer l’écriture chiffrée au cardinal d’une collection organisée. Il est important de favoriser la compréhension de l’itération de l’unité.

– La file numérique (parfois appelée le fil numérique car on utilise une corde à linge) : c’est une ligne numérique non tendue qui permet de faire le lien entre position et quantité.
N.B : Dans les pistes, bandes ou files, le zéro est souvent absent car il ne sert pas à dénombrer à ce stade. L’apparition du zéro avec la droite numérique marque ainsi une rupture dont l’enseignant doit avoir conscience.
– La ligne numérique est l’appellation courante de la droite numérique. Elle est orientée de la gauche vers la droite avec une graduation constante et a une origine.
2. Comment enseigner la droite numérique?
a) C’est un objet d’étude en lui-même
Selon J. Briand, avec la droite numérique, l’enfant est confronté pour la première fois à une symbolisation qui représente deux objets différents : il représente l’abscisse et la mesure algébrique (la distance entre le point repéré par l’abscisse et l’origine). C’est donc une représentation schématique inhabituelle qu’il faut enseigner en ayant conscience qu’elle met en jeu la numération mais également les mesures de longueurs.
Il prend l’exemple de 35.
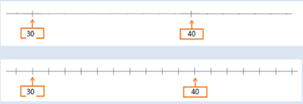
Le terme « entre » renvoie à une conception spatiale, alors que l’enfant a jusque-là à priori comparé des quantités, alors même que la droite n’a jamais été un objet d’enseignement.
Il s’agit alors d’y donner du sens : « 35 est entre 30 et 40 », «35 est au milieu de 30 et 40», «35 est à égale distance de 30 et de 40», « 35 est supérieur à 30 », «35 est moins loin du 0 que 40».
b) C’est un outil d’apprentissage
- En numération pour expliquer le rangement, les comparaisons, les encadrements, les décompositions (lien avec les réglettes Cuisenaire) de nombres entiers et nombres décimaux.

- En résolution de problèmes avec une double fonction : son utilisation est à la fois un moyen complexe mais efficace pour résoudre un certain nombre de problèmes additifs et une aide à la résolution des problèmes pour représenter la situation ou la solution du problème (lien avec le schéma en barre).
- En calcul pour donner du sens à la soustraction.
Je cherche à calculer 125-97. Il faut savoir que 125-97 me donne une longueur de bande sur la droite graduée. Pour connaitre la longueur de cette bande, il faut chercher à faire une soustraction moins compliquée que 125-97. En faisant glisser la bande de 3, j’obtiens 128-100 = 28. Cette méthode est un des prémices de la soustraction par le travail sur la conservation des écarts. L’enseignant aborde également la droite graduée ainsi que la notion de grandeur-longueur.


L’application Number Line peut être très utile pour accompagner cet accès au sens.
- En calcul pour donner une conception géométrique à la multiplication / la division. La graduation avec les multiples permet de visualiser la multiplication et de comprendre que 3 x 9 c’est 3 x 8 + 1 x 3. Ce travail permet également d’amorcer la division.


→ La recherche ACE propose comme fil rouge de l’enseignement mathématique en CP/CE1 l’apprentissage de la ligne numérique.

