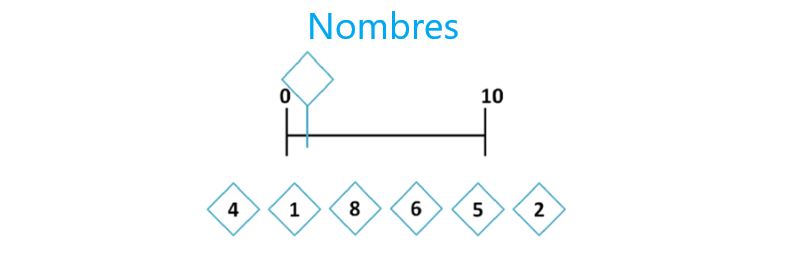
1/ Le concept de ligne numérique mentale
Dans le domaine de la cognition mathématique, se représenter mentalement le nombre, c’est en comprendre la magnitude, c’est-à-dire la quantité à laquelle il réfère. La ligne numérique mentale serait une représentation analogique construite dans le temps et évoluant pendant l’enfance jusqu’à aboutir à une forme adulte.
Le modèle du Triple Code (Dehaene, 1992) vise à expliquer les traitements numériques cognitifs de l’adulte, il postule que trois systèmes de représentation sont mobilisés pour le traitement du nombre, chaque type de représentation étant impliqué dans un traitement particulier du nombre.
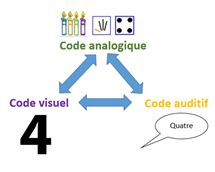
- La représentation visuelle arabe, qui correspond à la forme visuelle des nombres arabes, intervient dans les activités de calcul précis et permet de réaliser des calculs mentaux complexes.
- Le système auditivo-verbal est utilisé principalement dans l’activité de comptage.
- La représentation dite analogique, entrerait en jeu dans toute tâche nécessitant d’accéder à la quantité que représente le nombre, elle servirait donc à effectuer des comparaisons numériques et des calculs approximatifs.
C’est l’apport essentiel de ce modèle et ce sur quoi se base le concept de ligne numérique mentale. Seul le code analogique contiendrait l’information sur la quantité.
Selon S. Dehaene, les différents nombres seraient alignés mentalement sur une ligne où chaque position correspondrait à une certaine quantité : nombres ordonnés de gauche à droite dans la culture occidentale en lien avec le sens de la lecture et avec une relation nombres-espace.
L’enfant accorderait plus d’espace entre les petits nombres qu’entre les grands nombres. Cette ligne numérique subjective ressemblerait donc à ceci :
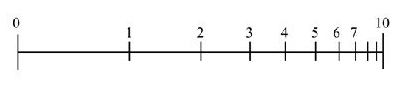
La linéarité n’est construite que vers 9 ans (espaces équivalents). Il n’y a pas de « droite mentale innée » dont les écarts deviendraient réguliers. Pour que les élèves apprennent que l’écart entre deux nombres qui se suivent est constant et égal à 1, il est nécessaire d’insister sur la différence entre comptage-numérotage et comptage-dénombrement et sur le rôle fondamental de l’itération de l’unité comme le rappelait Rémi Brissiaud.[1]
2/ La ligne numérique physique : du discret au mesurable
Un nombre désigne à la fois un point (l’abscisse) et la distance à l’origine (la mesure algébrique : aspect métrique).
Il existe un lien entre le nombre et l’espace.
Sur une ligne numérique, les unités sont présentes mais la façon dont les chiffres en désignent les quantités est particulièrement obscure. Ainsi, dans le haut du schéma ci-dessous on comprend facilement le rapport entre unités et chiffres, alors que sur la ligne numérique du bas il devient moins clair.
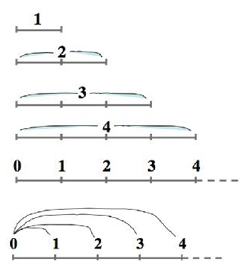
Deux opérations de pensée sont nécessaires pour passer des quatre représentations du haut à la ligne numérique du bas tout en continuant à donner du sens à cette représentation :
– la ponctualisation : comprendre que les chiffres ont été déportés vers l’extrémité de droite plutôt que de rester centrés sur la quantité qu’ils représentent.
– l’inclusion des quantités : « fusionner » les différentes représentations du haut de façon à inclure les différentes quantités l’une dans l’autre.
Ces deux opérations de pensée sont en effet la clé d’un usage réfléchi de cet outil.
3) En quoi le test des évaluations nationales CP s’avère utile ?
L’exercice « associer un nombre à une position sur une ligne numérique » dans les évaluations nationales CP est un exercice difficile. C’est une représentation schématique qui demande une culture de la droite numérique. Un schéma, ça s’apprend. C’est un système de lecture, avec des icônes qui nécessite un apprentissage.
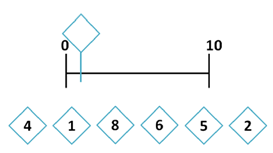
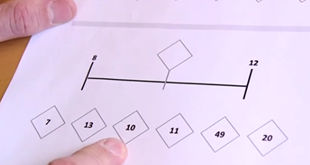
→ Alors pourquoi le proposer à de jeunes élèves ?
Selon le CNESCO, les travaux qui consistent à demander à de jeunes enfants de placer sur un segment borné de 0 à 10 des grandeurs ou des quantités symboliques (1, 3, 7, …) présentent une double orientation :
– théorique en vue d’évaluer dans quelle mesure les représentations mentales se conforment à une forme linéaire;
– pragmatique afin de définir un indice du niveau de développement des compétences numériques définies en termes de représentations ou de stratégies.
Dans une vidéo d’explicitation de ce test sur Eduscol, il est précisé que, d’après de nombreuses recherches, il est très important et utile pour les enfants de comprendre la correspondance entre le nombre et l’espace. L’idée que les nombres peuvent mesurer l’espace ne va pas de soi et le fait de dire que les quantités peuvent être mises en correspondance avec l’espace constitue un point fondamental qui va ensuite servir à tout l’échafaudage des mathématiques : pour la construction future des nouveaux nombres que sont les décimaux, pour comprendre le sens de l’addition (déplacement vers la droite sur la ligne) ou de la soustraction (déplacement vers la gauche) ou encore pour préparer la construction des coordonnées en géométrie (l’idée que les nombres peuvent servir à mesurer des positions de points sur un graphique).
Tout ceci est ainsi anticipé dans ces tests de la ligne numérique qui sont en quelque sorte des petites résolutions de problèmes qui permettent à l’élève de raisonner, d’approximer et à l’enseignant d’évaluer la compréhension profonde du sens des nombres chez l’élève.
Au regard des dernières recherches (Méta-analyse, Schneider et al., 2018), un travail sur l’estimation à partir de cette ligne numérique permettrait rapidement aux élèves d’améliorer leurs performances en comptage et arithmétique.
[1] http://www.cafepedagogique.net/lexpresso/Pages/2018/10/19102018Article636755319854215458.aspx