La corde à treize nœuds parfois appelée « corde des druides » ou « corde égyptienne » était un outil utilisé dans l’Egypte antique et l’un des outils essentiels des bâtisseurs du Moyen Âge qui auraient ainsi transmis leurs ordres de construction même aux ouvriers ne possédant que peu de connaissances dans les domaines de la géométrie et du calcul.
C’est une corde composée de 13 nœuds qui séparent 12 intervalles réguliers (12 intervalles de longueurs identiques). Le nœud est un repère sur la corde, marquant un espace, comme le fait la graduation sur une règle entre chaque centimètre … le nœud n’est pas une mesure de longueur, c’est une graduation.

Cet outil semble permettre l’enseignement de nombreuses notions mathématiques dans des classes de cycle 2 et de cycle 3.
- Un instrument motivant pour l’enseignement :
L’intérêt de l’outil « corde à treize nœuds » réside dans les aspects suivants :
· la motivation des enseignants comme des élèves, née de la curiosité pour cet outil nouveau dans les pratiques scolaires actuelles mais pourtant historiquement très ancien;
· la possibilité de relier connaissances dans l’espace réel et modélisation par la géométrie;
· la différenciation implicite entre dessin et figure, fondamentale pour la géométrie (ex. il existe un losange de côté 3 unités et il existe une infinité de dessins différents de ce losange).
D’autres développements sont possibles, notamment pour explorer des connaissances liées au cercle ou encore des connaissances du domaine numérique.
L’intérêt historique[1] est également non négligeable pour que les élèves puissent percevoir le long cheminement de la construction des connaissances, en lien notamment avec les outils dont dispose une communauté à un moment donné de son histoire.
2. Un outil générateur d’apprentissages
La corde à 13 nœuds est un outil dont les multiples usages permettent de faire rencontrer aux élèves des notions :
· dans le domaine de la géométrie, il est un puissant outil : figure plane (triangle rectangle, triangle isocèle, triangle équilatéral, carré, rectangle, losange peuvent notamment être matérialisés par la corde), figure dans l’espace, alignement, segment, droite, cercle, orthogonalité, parallélisme, polygones, symétrie, milieu.
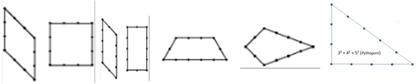
La corde permet de visualiser le carré ou le losange par la répétition de 4 nombres identiques (3+3+3+3), les rectangles ou parallélogrammes par la répétition d’une paire de nombres (1+5+1+5 et 2+4+2+4) , les trapèzes isocèles par un même nombre à deux places non consécutives (1+3+5+3 ou 2+3+2+5), le triangle équilatéral (4+4+4) ou le triangle isocèle (2+5+5) qui compte cinq intervalles sur deux de ses côtés et deux intervalles sur sa base ou le triangle rectangle (3+4+5) avec son angle droit et ainsi découvrir les propriétés permettant de différencier les figures entre elles.
· dans le domaine des grandeurs et mesures : longueur, périmètre, aire, existence d’un polygone de dimensions données (inégalité triangulaire);
. dans le domaine numérique : décomposition additive du nombre 12, comparaison de nombres,… La corde à 13 nœuds permet d’additionner, soustraire, multiplier, diviser sans calcul ! Par exemple, plier la corde de façon à avoir, sur chaque pli, quatre intervalles, permet d’observer que 3 plis fois 4 intervalles = 12 intervalles. Elle est aussi un autre prétexte pour travailler les fractions.
3. Un lien pour passer du méso-espace au micro-espace
- Dans le méso-espace, ou espace qui peut être embrassé par un sujet par un regard circulaire, il s’agit d’une corde similaire à celle utilisée historiquement d’une longueur d’environ 6m.

Elle sert alors d’instrument de vérification et de tracé, et nous retrouvons là son usage en tant qu’outil des bâtisseurs utilisé jusqu’au Moyen Age : tracer des dessins géométriques à partir des pré-figures, réaliser des traits droits, réaliser ou vérifier un alignement, comparer des longueurs ou réaliser une longueur multiple d’une autre, réaliser ou vérifier l’orthogonalité, réaliser ou vérifier un parallélisme.
- Dans le micro-espace, espace constitué par l’environnement proche d’un sujet qui peut être vu et touché sans avoir à se déplacer, cette grande corde est remplacée par deux outils différents :

Avec les cordelettes, on peut par exemple faire tracer un cercle de rayon donné (ex: le rayon fait 2 espaces ou comprend «3 nœuds»), construire un triangle, des triangles, écrire un message pour le faire construire par d’autres élèves.
Avec les cordes-pailles : on peut faire rechercher le périmètre des figures en unités paille, montrer qu’elles ont le même périmètre mais qu’elles sont de formes différentes. Un travail similaire relatif aux aires peut être mené.


1 Pingback