Le mot du chercheur : enseigner hors la classe (juin/juillet 2021)

En 2002, Dominique Bucheton affirmait « Je crois profondément qu’apprendre, c’est se déplacer (…). Pour que les enfants apprennent, et j’en suis de plus en plus convaincue, il faut créer des situations didactiques où les déplacements soient en même temps cognitifs, intellectuels, psychoaffectifs, identitaires, langagiers ». (Extrait de Devenir l’auteure de sa parole Eduscol janvier 2002)

A travers la ressource Mathscitymap, nous nous sommes interrogés sur l’impact d’une activité hors les murs sur l’apprentissage des mathématiques.

1. Qu’est-ce qu’enseigner hors les murs ?

Se déplacer induit de facto sortir de la classe mais « sortir », en soi, n’est pas forcément gage d’apprentissage tel que le conçoit l’école. En effet, en se référant aux travaux de Tricot et Sweller, on peut catégoriser 2 types d’apprentissages : les connaissances primaires et les connaissances secondaires.

Ainsi, la sortie « plein air » devient un outil didactique au service des apprentissages. En mathématiques, il s’agira de contextualiser les savoirs dans le but de les rendre accessibles et concrets pour les élèves. On ne va pas se balader seulement pour le plaisir, on s’attelle à intégrer les mathématiques dans le quotidien, dans les savoirs collectifs, dans la culture générale. L’objectif poursuivi est d’ancrer les apprentissages dans le réel soit en confrontant les compétences au réel soit en partant du réel pour acquérir des compétences.

2. Pourquoi enseigner hors la classe ? une approche des neurosciences

Les sciences cognitives ont identifié quatre facteurs principaux de réussite d’un apprentissage : l’attention, l’engagement actif, le retour d’information, et enfin, la consolidation.

• L’attention, un filtre qu’il faut savoir captiver et canaliser : il nous permet de sélectionner une information et d’en moduler le traitement.

Le support de travail qui est « concret », des modalités de travail par petit groupe où chacun a sa place, complétés par du temps et des allers-retours avec la classe pour mieux comprendre les enjeux des savoirs dans la vie courante et les transférer dans d’autres situations peuvent être des stimuli face à la tâche demandée.

• L’engagement actif : le principe directeur est on ne peut plus clair : un organisme passif n’apprend pas.

L’enseignant ne peut mobiliser que si l’enfant ou apprenant se mobilise.

En diversifiant les modes d’approche, on crée aussi de la motivation et chez certains élèves la sortie pourra créer un déclic et donner du sens aux apprentissages. C’est une mise en rapport de l’élève avec l’objet math dans un contexte différent.

Une activité de plein air favorise l’engagement de toute la personne de l’élève avec tous ses sens, pas seulement la vue et l’ouïe comme en classe, mais aussi son toucher, son odorat et encore sa sensibilité et son affect. (Amiel & Ferrerons, 2013).

• Le retour d’information : si l’activité plutôt qu’une écoute passive est capitale, elle ne suffit pas. Pour l’élève,

ce retour réflexif est une voie propice pour accéder à une meilleure compréhension de la notion étudiée. Par ce travail, il découvre aussi son propre fonctionnement intellectuel et gagne en autonomie. Pour l’enseignant, cela permet de découvrir les démarches d’apprentissage des élèves, d’identifier leurs besoins, de différencier les approches pédagogiques, de les évaluer avec pertinence.

• La consolidation et l’automatisation : pour combattre l’oubli et consolider dans un temps long, l’élève doit pouvoir étudier la même notion à plusieurs reprises. C’est au prix de cette répétition dans le temps de l’apprentissage qu’il acquerra des connaissances qu’il pourra mobiliser des années plus tard.  En ce sens, une approche en plein air est un levier pour permettre à l’élève de voir/revoir/re-revoir et ancrer durablement les notions, les savoirs dans le temps long, et dans d’autres contextes.

3. Les mathématiques en plein air, un moment en rupture avec les temps habituels en classe qui profite aux apprentissages mathématiques 

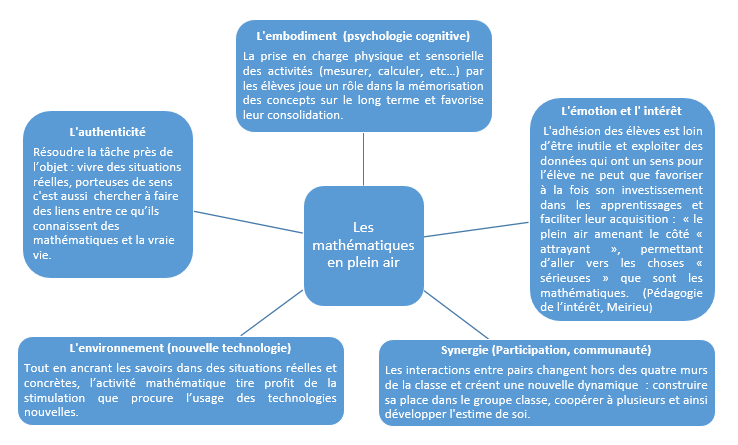
Matthias Ludwig, chef du projet Math City Map à l’Université de Francfort a donné le 15 mai 2019 à l’IREM de Paris le résultat des études menées sur l’utilisation de cette application. Une synthèse d’études américaines (Kuo, Barnes et Jordan 2019) a également pu démontrer plusieurs effets de la pratique hors la classe de l’enseignement.