Faire des mathématiques, c’est résoudre des problèmes en développant un raisonnement. Pour que cette activité cognitive puisse avoir lieu, le problème proposé doit répondre à de nombreuses caractéristiques comme notamment être engageant et consistant.
L’activité du napperon présentée dans la ressource est une activité aux nombreux potentiels didactiques. Vécue comme une situation de référence pour la classe ou pour les formés, elle met en jeu la notion de symétrie comme réponse au problème posé, met en avant le rôle de l’anticipation et de la manipulation active au service des apprentissages.
- La symétrie axiale comme réponse au problème posé
Il n’y a pas de définition formelle de la symétrie mais elle se définit plutôt par l’action.
Il est important de travailler à l’école élémentaire sur des figures avec axe(s) et des figures sans axe de symétrie dans l’apprentissage de la symétrie axiale. Pour qu’une forme soit reconnue comme ayant un axe de symétrie, il faut qu’elle soit perçue comme un tout. L’observation de la nature permet aux élèves de comprendre que la symétrie est présente dans notre environnement et de comprendre aussi cette notion de tout.

Produire de la symétrie par pliage et découpage, par pliage et traces de peinture ou papier calque dès les petites classes constituent les premiers jalons pour construire avec les élèves le concept d’axe de symétrie (l’axe de symétrie vérifiant la propriété suivante : si on plie la figure suivant cet axe, les deux moitiés de figures se superposent).
Pour M.J Perrin (APMEP, Grenoble 2011), on peut penser la continuité de l’organisation mathématique en lien avec les apprentissages selon deux dimensions :
• les actions et les types d’objets (matériels ou non) sur lesquels elles s’exercent, en lien avec les concepts géométriques gouvernant la symétrie ;
• les deux aspects de la symétrie axiale, soit comme propriété d’une figure soit comme transformation d’une figure en une autre.
Dans l’activité du napperon préconisée comme remédiation à l’évaluation de début de 6ème par Eduscol, la symétrie intervient comme réponse à la situation problème. Le nombre d’axes repérés sur la figure modèle va engendrer les pliages et les découpes pour réaliser correctement le napperon.
2. Le rôle des essais-erreurs et de l’auto-validation des apprenants
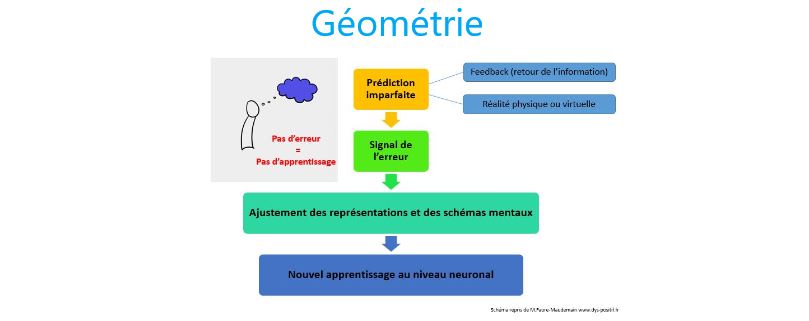
Le rôle positif donné à l’erreur : l’erreur dans les modèles constructivistes est considérée comme une étape de l’apprentissage, nécessaire et source d’enseignements pour tous. En effet, c’est bien souvent en analysant une production erronée qu’il est possible de prévoir ce qu’il faudrait faire pour obtenir tel ou tel résultat.
Pour M.L Peltier (2003), les essais erronés dans l’activité du napperon sont intéressants à conserver car ils ont 2 fonctions :
– La première est de permettre à son auteur de mener une réflexion et une analyse fine des effets d’un découpage sur un papier plié en 2, en 4, ou en 6. L’erreur peut alors être un point de départ pour affiner la réflexion : en analysant l’effet de telle découpe sur le papier déplié, l’élève fera des hypothèses sur les modifications à effectuer pour obtenir le résultat souhaité.
– La seconde provient du fait que tous les napperons obtenus qu’ils soient ou non conformes au modèle, présentent des axes de symétrie, et constitueront donc un matériel intéressant pour entrainer les élèves à repérer des axes de symétrie dans des figures variées.
Les neurosciences nous apprennent que c’est de l’erreur que naît l’apprentissage : le fait de focaliser sur ces erreurs et de chercher des solutions pour les corriger (donc de faire de nouvelles prédictions) va déclencher l’apprentissage. Il faut donc aider les élèves à centrer leur attention sur leurs stratégies et les ressources qu’ils ont en eux pour surmonter leurs erreurs. C’est ainsi qu’ils pourront apprendre.
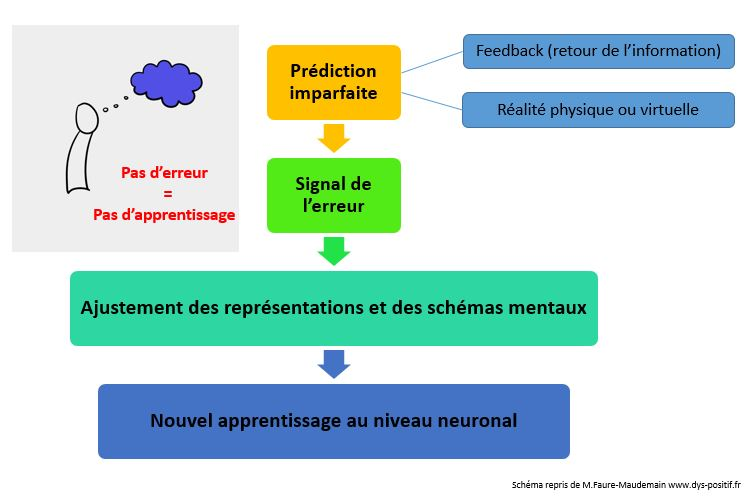
L’auto-évaluation : Dans cette activité, la validation est à la charge de l’élève. Elle se fait par confrontation visuelle au modèle. Les réalisations obtenues ne sont pas superposables au modèle, ce qui doit être respecté, ce sont les formes géométriques des découpes, leur nombre, leurs positions relatives, leur orientation. Si pour certains élèves cette auto-validation n’est pas assurée, le professeur devra jouer son rôle de médiateur.
3. Le rôle de la manipulation active comme support pour l’anticipation
Dans la première phase de manipulation libre, les élèves s’engagent dans la tâche de reproduction, la main travaille, mais l’esprit est peu sollicité. Au moment de l’observation des réalisations, certains élèves peuvent développer une activité de pensée en cherchant à justifier les constats qu’ils peuvent faire, mais cette activité n’est pas à proprement parler requise pour réaliser la tâche demandée. On parle ici de manipulation passive.
Dans la deuxième phase, lorsqu’il s’agit de reproduire le modèle, l’esprit est mobilisé en même temps que la main. L’enfant développe une réelle activité cognitive, il anticipe son action, il la prévoit ; la manipulation sert à réaliser matériellement cette anticipation et à la valider. C’est dans cette deuxième phase que l’on peut parler d’activité mathématique et de manipulation active.
Rappelons ici le triptyque Manipuler-Verbaliser-Abstraire fondamental pour toute activité mathématique.
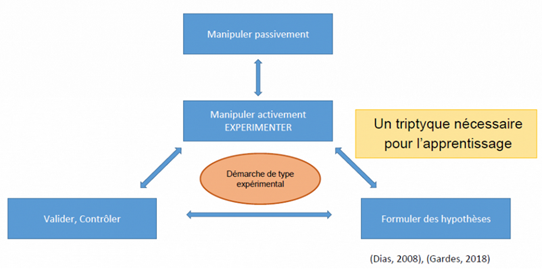
Ainsi, dans l’activité du napperon, les manipulations ont 3 fonctions :
– La manipulation permet une accumulation d’expériences qui, pour être disponibles par la suite, ont à être décrites et surtout évoquées après avoir été conduites. Cette évocation différée participe à la constitution d’images mentales. Accumuler des expériences, c’est aussi construire des relations entre ces expériences et ne pas les considérer comme des éléments isolés. C’est par le langage que ces expériences seront cognitivement efficaces.
– La manipulation peut être un support pour la pensée dans le cadre de l’anticipation de l’effet d’une action, d’une transformation ou dans le cadre de l’élaboration et du développement d’un raisonnement. Pour réussir, l’élève est invité à mener une manipulation mentale qui prend appui sur des faits déjà vécus a priori et mémorisés.
– La manipulation permet une validation pragmatique des hypothèses formulées dans le registre du raisonnement sur les images mentales construites et des démarches de résolution élaborées afin de les éprouver.