Les programmes et instructions officielles prescrivent un enseignement spécifique du calcul mental à l’école élémentaire. Inspirée par le rapport Villani-Torossian de 2018, la note de service du 25 avril 2018 relative à la priorité au calcul en pose le cadre : « Que ce soit sous forme d’activité décrochée de la séance de mathématiques ou bien intégrée à celle-ci, oralement, sur l’ardoise, sur feuille ou sur le cahier de brouillon, avec un support oral (le maître dicte) ou écrit (tableau noir, TBI, tablettes, ordinateurs, fiches, etc.), le calcul mental doit faire l’objet d’une pratique quotidienne moyenne d’au moins 15 minutes. On privilégiera l’alternance de séries de séances d’entraînement courtes (10 à 15 minutes) avec des séances longues (30 à 45 minutes) visant des apprentissages procéduraux spécifiques. »
Mais qu’entend-on exactement par calcul mental ? Comment mettre en place un enseignement efficace ?
- Le calcul mental : des faits arithmétiques et des calculs stratégiques (définitions) [1]
Le calcul mental se définit comme le calcul qui s’effectue dans la tête. Ce calcul numérique ne passe pas par des intermédiaires écrits mais peut faire appel à des supports visuels (bande numérique, tableau de nombres, …).
Il peut être oral (l’élève dit le résultat) ou écrit (l’élève écrit alors le résultat et seulement le résultat). L’énoncé peut être oral ou écrit (permanent ou temporaire). Il n’est pas exclu d’utiliser l’écrit pour la correction et garder une trace.
S’il se distingue du calcul en ligne, du calcul posé et du calcul instrumenté, il est néanmoins présent dans tous ces moyens de calculer.
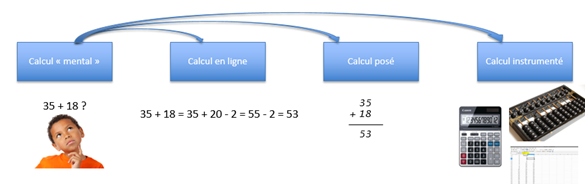
Le calcul mental se divise en deux grandes catégories :

Cette catégorisation s’explique notamment par l’activité de notre cerveau pendant l’activité de calcul mental. En effet, pour acquérir des automatismes, le cerveau active deux types de mémoire dissociés reposant sur des régions cérébrales différentes :

Les automatismes en mémoire déclarative ou procédurale sont complémentaires et ont plusieurs points communs :
- Ils nécessitent la pratique répétée ;
- Ils se construisent avec l’apprentissage des faits arithmétiques, mais aussi avec la pratique du calcul mental stratégique ;
- Leur construction ne s’oppose pas à l’apprentissage du sens.
A ce titre, une étude comparative a prouvé que la méthode la plus efficace pour l’acquisition d’automatismes est le couplage de l’apprentissage par comptage ( en s’appuyant sur une ligne numérique ou les doigts) à l’apprentissage par cœur.[2]
Pour plus de détails sur l’enseignement des faits numériques, nous vous renvoyons à notre article de mai 2020.
2. Comment mettre en place un enseignement efficace du calcul mental ?
Tout d’abord, les objectifs de l’enseignement du calcul mental sont l’acquisition d’automatismes pour libérer de la mémoire de travail pour des tâches plus complexes et viser des stratégies efficientes et efficaces.
– On peut définir une stratégie efficace par le fait que la stratégie utilisée nous amène au bon résultat. Or, le calcul mental s’inscrit dans une logique temporelle : du fait de la forte charge de mémoire, il faut être rapide pour réaliser les calculs.
– Une procédure efficiente est une procédure qui va aboutir au résultat en minimisant le plus possible la charge en mémoire de travail, c’est-à-dire en limitant le coût cognitif.
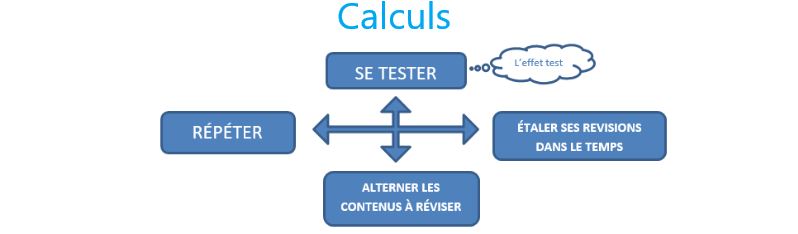
De plus, la recherche actuelle montre que l’apprentissage en général et celui du calcul mental en particulier doit reposer sur 4 grands principes pour permettre à l’élève d’apprendre et de mémoriser efficacement :
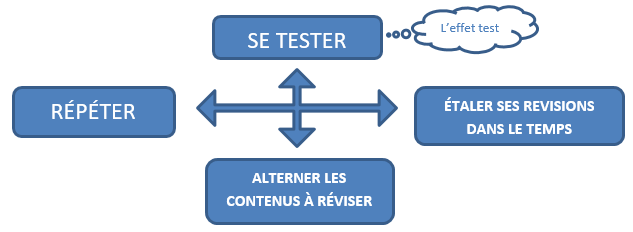
– RÉPÉTER : pour favoriser l’automatisation; pour favoriser la création de traces en mémoire et la récupération de faits arithmétiques; pour favoriser l’automatisation de procédures et alléger la mémoire de travail.
– SE TESTER (« l’effet test ») : se tester de manière fréquente avec un retour immédiat sur l’erreur; se tester pour apprendre et non pour être évalué; tester même les faits déjà appris; chronométrer pour favoriser la « fluence » de calcul.
– ÉTALER SES RÉVISIONS DANS LE TEMPS : les activités de calcul mental doivent être étalées sur de longues périodes et non massées; importance de les ritualiser.
– ALTERNER LES CONTENUS À RÉVISER : alterner les types de problèmes travaillés au sein même des séances de calcul mental; alterner aussi avec d’autres activités maths ou avec des activités autres que mathématiques.
Pour enrôler les élèves dans les activités de calcul mental, il est enfin nécessaire d’ajouter un aspect ludique, de recherche de défis au-delà de la seule délivrance de faits ou procédures automatisés. La pratique régulière en classe, les échanges « d’astuces » amènent la création d’un répertoire qui encourage l’élève à développer le goût du nombre et des opérations.
Quelle jubilation pour un élève de comprendre que la multiplication de 25 par un nombre à plusieurs chiffres multiples de 4 est d’une facilité déconcertante pour peu de l’avoir appris ensemble ! (36 X25 = 9X 4X25= 900)
[1] Source : intervention de Jérôme Prado janvier 2022, PNF RMC
[2] Fuchs et al (2010) Learning and Individual Differences