Si l’intérêt d’utiliser le jeu dans l’enseignement des mathématiques n’est plus à démontrer (cf. m@ths+ précédent), jouer étant une des quatre modalités d’apprentissage, il nous a semblé intéressant, à travers la présentation du jeu de l’awélé de voir à quel point l’anticipation est au cœur du raisonnement mathématique.
- L’anticipation : une compétence essentielle en mathématiques
L’anticipation se définit comme le mouvement de la pensée qui imagine ou vit d’avance un évènement. C’est une habileté cognitive qui est concomitante avec la capacité d’abstraction.
Or, faire des mathématiques, c’est abstraire le réel. En effet, les mathématiques utilisent des symboles, des formules et des théories pour modéliser des phénomènes réels et résoudre des problèmes complexes.
Pour arriver à l’abstraction, un élève a besoin, dans un premier temps, de manipuler des objets concrets, physiquement. Mais la seule manipulation ne fait pas comprendre les concepts. Intervient donc dans l’enseignement le fameux triptyque « manipuler, verbaliser, abstraire » mis en exergue par le rapport Villani Torossian.
Dans le deuxième épisode « perspective sur » la méthode Singapour produit par la DGESCO, Kévin Gueguen explique que, parmi les critères clés d’un matériel de manipulation, il faut que le matériel ou la situation amène la possibilité de « parler sur » le concept. Et c’est bien tout l’enjeu d’une manipulation efficace pour abstraire !
Parler sur, c’est donner la parole à l’élève non seulement sur ses actions réalisées mais aussi permettre à l’enfant de poursuivre son raisonnement, structurer sa pensée en le questionnant. L’anticipation est alors au cœur des interrogations : comparaison des actions possibles avec résultats anticipés : « que se passerait-il si ? »
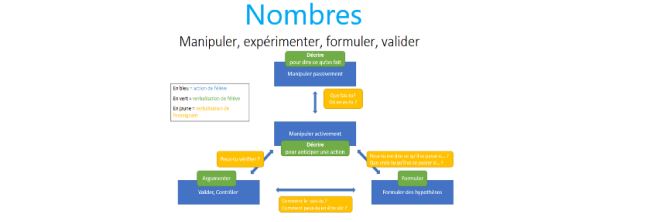
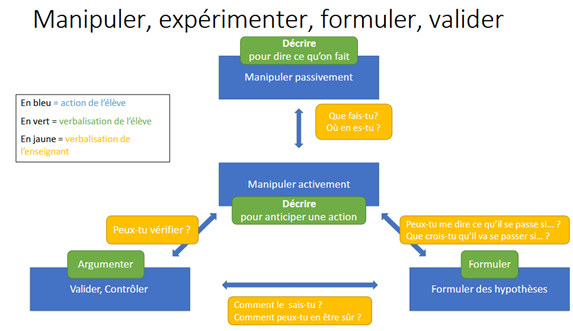
Marie-Line Gardes, Professeure HEP ordinaire en didactique des mathématiques, dans le schéma ci-dessous, met en avant le rôle de l’adulte (en jaune) dans l’accompagnement de l’élève. C’est bien le questionnement d’anticipation des actions qui amène à une manipulation active de l’élève c’est-à-dire une manipulation au service d’un apprentissage mathématique.
Appliquée aux mathématiques, l’anticipation permet de :
- prévoir les résultats : valider ou invalider le recours à une stratégie
- planifier les étapes : valider ou invalider le recours à une stratégie
- recourir à des savoirs et savoir-faire.
2. De l’anticipation à la stratégie
Dans une note du conseil scientifique de l’éducation nationale intitulée « l’ouverture des mathématiques à l’école maternelle et au CP », S. Dehaene explique qu’on pourrait définir les mathématiques comme “la science des régularités” (the science of patterns). Partout où il y a des règles précises, et où l’on réfléchit aux conséquences logiques de ces règles, il y a des mathématiques. L’être humain trouve du plaisir à découvrir ces règles et leurs conséquences parfois inattendues, et à les expliquer à d’autres.
Dans le cadre de jeu de règles en classe, tel que l’awélé, c’est exactement ce qui est visé.
Analysons dans un premier temps les actions du joueur novice.
Il procède en général de façon aléatoire, il part de l’expérience. De manière empirique, il va accumuler les parties pour développer des stratégies et procédures en évaluant les conséquences de ses actions et en les ajustant.
Au fur et à mesure, il va délaisser ses pratiques empiriques au profit de simulations mentales sans avoir besoin de les tester systématiquement en actes.
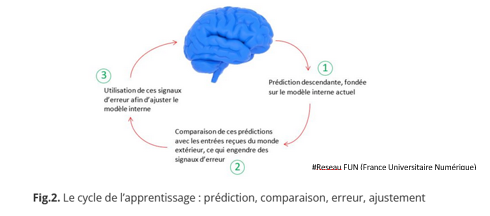
Le joueur devient alors plus expert, il s’épargne un grand nombre de tests inutiles et apprend à anticiper ses actions et celles de l’autre joueur.
Plus il développe sa capacité à anticiper, plus il a de chance de gagner.
Mais rien n’indique que le joueur novice se lance seul dans l’anticipation. Il peut décider de poursuivre une stratégie aléatoire jusqu’à la victoire attendue. De plus, l’élève constate souvent des faits mais n’arrive pas à aller plus loin.
Interroger l’élève, l’amener à anticiper c’est lui faire dire à haute voix comment il arrive à un résultat même s’il doit sa solution à sa bonne intuition. Celle-ci est forcément induite par un vécu et des savoirs a priori.
L’élève doit rechercher ce qui, dans sa stratégie, lui a permis d’atteindre son but et découvrir a posteriori le procédé efficace qu’involontairement il a mis en œuvre.
Le rôle du PE va être prépondérant pour amener l’élève à se saisir de prédictions intuitives comme véritables enjeux mathématiques (cf. Théorie des situations Brousseau).
Le jeu l’a amené à oser, tenter, essayer, prendre des risques, faire des erreurs et des choix assumés… ce qui est indispensable aux apprentissages.
Un temps de réflexion et d’analyse sur la fonction du jeu est primordial. Tout comme il doit y avoir un avant-jeu et un après-jeu, il est nécessaire de prévoir des arrêts sur partie (autrement dit des situations de « jeu arrêté ») pour analyser au mieux les différentes possibilités offertes et apprendre à optimiser son tour de jeu. La notion de gain et de perte doit toujours être rapprochée de l’objectif mathématique, et donc relativisée. L’élève doit toujours être conscient de l’intérêt en termes d’apprentissage et des transferts possibles dans des activités de résolution de problèmes et de recherche notamment.