Quelques points cruciaux liés aux difficultés soulevées par l’apprentissage de l’arithmétique élémentaire :
- La première difficulté majeure tient au passage au symbolique : la mise en correspondance des quantités avec des systèmes de symboles (qu’il s’agisse de la suite orale des noms de nombres, des configurations de doigts, des abaques ou des chiffres arabes) pose problème à tous les enfants ;
- La deuxième difficulté a trait au passage des transformations (analogiques) aux opérations (symboliques) ;
- La troisième difficulté réside dans le calcul mental : le lien entre le calcul mental et la réussite scolaire est bien établi par la recherche (voir par exemple Suchaut et Morlaix, 2007). Cela s’explique aisément : le calcul mental est un domaine privilégié pour permettre aux élèves de s’approprier les connaissances conceptuelles qui sont indispensables à la résolution de problèmes arithmétiques.
https://media.eduscol.education.fr/file/ecole/00/3/Le_nombre_au_cycle_2_153003.pdf
Les réglettes Cuisenaire : un matériel didactique qui donne accès au rapport entre les nombres et à leurs propriétés, quelle que soit leur valeur numérique, qui présente les structures de base de l’arithmétique et de l’algèbre élémentaire (Madeleine Goutard).

- 3 moyens d’appréhension
Les neurosciences ont démontré que notre réflexion est optimisée lorsque celle-ci active plusieurs de nos sens. Et en mathématiques, cela prend tout son sens. En effet la manipulation sensorielle d’un matériel, adapté au développement cognitif, facilite la conceptualisation des notions plus abstraites. C’est le cas des réglettes Cuisenaire avec lesquelles la vue, le toucher et l’ouïe sont sollicitées. La mémoire visuelle, la mémoire auditive, et la mémoire tactile interviennent, pour chaque enfant, suivant sa meilleure sensibilité. La mise en action de ces trois types de mémoire permet d’activer ces différentes facultés, d’accélérer le processus d’apprentissage, et de compenser l’une ou l’autre déficience de perception.
2. Un processus d’apprentissage : découverte et vérification
Les réglettes Cuisenaire ont un statut spécifique parmi les aides à l’apprentissage du calcul puisqu’elles ne sont pas des collections témoins organisées comme les configurations de doigts ou les constellations. Alors que les constellations se bornent à illustrer les relations numériques, les réglettes Cuisenaire se présentent comme un moyen de vérifier ces relations numériques : l’enfant qui pense que 4+3=8 et qui connait bien le code couleur « 4 c’est violet, 3 c’est vert et 8 marron » peut procéder à la schématisation. Comme la règle marron dépasse, il prend conscience de son erreur. Il peut alors émettre l’hypothèse que 4+3=7 et vérifier cette nouvelle hypothèse.
Les élèves deviennent aptes à analyser leurs erreurs, à les éviter par anticipation et à évaluer leurs besoins d’aide. Toute la pédagogie d’essai et erreur peut prendre place avec ce matériel qui favorise l’anticipation et est autocorrectif
3. Une priorité : donner du sens au nombre
- Le matériel Cuisenaire évite de tout rapporter à l’unité et permet de focaliser le raisonnement sur les rapports entre les réglettes et donc entre les nombres. Georges Cuisenaire savait que faire de la mathématique c’était abstraire et raisonner. Son expérience d’enseignant lui apprit que la pensée opératoire ne travaillait pas sur des nombres mais sur des rapports, des relations entre grandeurs caractérisées par les notions d’équivalence, c’est-à-dire d’égalité, d’ordre et d’algèbre (ROBICHAUD Cécile, L’efficience des réglettes Cuisenaire). Les enfants manipulent des réglettes qui symbolisent les nombres pour rendre concret leurs relations (première approche des réglettes et des nombres qu’elles représentent en observant leur longueur et leur couleur, pas de valeur numérique dans un premier temps).
- Cet ensemble de dix réglettes s’ajustent si bien les unes avec les autres que l’enfant découvre sans s’en apercevoir qu’il y en a des plus grandes, des plus petites, que certaines ont une longueur double d’autres, que certaines s’associent judicieusement. Les différences particulières qui existent entre elles permettent de symboliser les opérations et les propriétés des nombres et de s’en faire des images mentales. On a visuellement une relation très claire du rapport entre les premiers nombres.
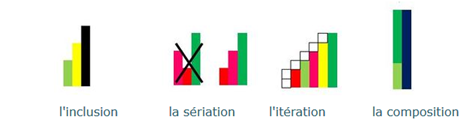
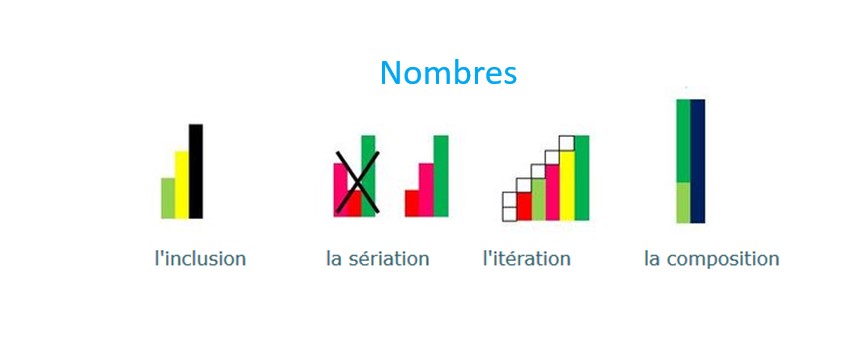
Ce qui donnera du sens au nombre :

Par sa manipulation, les différentes opérations mathématiques auxquelles l’enfant aura recours dans un deuxième temps auront déjà été vécues. « Toutes les opérations mathématiques sont présentées comme des aspects des jeux auxquels il a joué avec les réglettes, en sorte qu’un accroissement continu et cohérent de clarté se manifeste à mesure que se développe son intuition mathématique. » GATTEGNO Caleb.
Il est à souligner que Rémi Brissiaud s’est largement inspiré des réglettes Cuisenaire pour introduire ses « Noums » en CP. Cela permettrait aussi selon lui de favoriser le recours à la construction de schémas (de type schéma en barre notamment) plutôt qu’à des schémas conventionnels utilisés mécaniquement.
http://www.cafepedagogique.net/lexpresso/Pages/2018/06/29062018Article636658542946041670.aspx