Dès l’entrée en maternelle, les apprentissages sont structurés autour d’un enjeu de formation central pour les enfants « apprendre ensemble et vivre ensemble ». Les enfants se construisent comme personnes singulières et découvrent le rôle du groupe dans ses propres cheminements, en participant à la réalisation de projet collectif, en apprenant à coopérer (extrait BO 24 juin 2021 école maternelle).
Coopérer et réaliser des projets convoquent tous les domaines et la coopération est une compétence à acquérir.
Mais qu’entend-on réellement par coopération ? Comment la mettre en place ? Quel impact dans l’enseignement des mathématiques ?
- La coopération
La coopération désigne l’« action de participer (avec une ou plusieurs personnes) à une œuvre ou à une action commune », ou l’« aide, [l’]entente entre les membres d’un groupe en vue d’un but commun ».[1]
A l’école, « le terme approche coopérative [est utilisé] pour désigner un ensemble de méthodes dont l’enjeu est d’organiser une classe en sous-groupes, au sein desquels les élèves apprennent ensemble et travaillent en coopération sur des tâches scolaires. »[2]
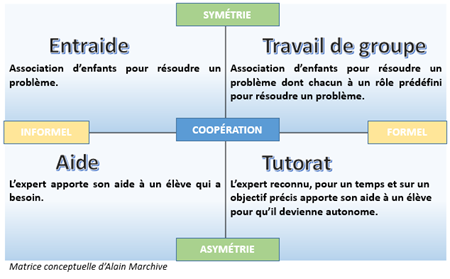
En s’appuyant sur les travaux d’Alain Marchive, Sylvain Connac définit les quatre formes de coopération à l’école.
Coopérer, c’est : aider, s’entraider, travailler en groupe, rentrer dans des logiques tutorielles.
Chaque forme a des caractéristiques propres. L’entraide et l’aide sont souvent spontanées, non structurées à l’inverse du travail de groupe et du tutorat qui requièrent une organisation. Le niveau de compétences joue lui aussi un rôle créant des relations symétriques (entraide, travail de groupe) ou asymétriques (aide et tutorat).
Il est donc important de varier les formes de coopération au sein de la classe.
Afin de bien percevoir les enjeux de la coopération, il est nécessaire de la distinguer de la collaboration.
En effet, Philippe Meirieu a très vite alerté sur les dérives possibles du travail collaboratif (travail de groupes avec projet commun) qui engendre une division du travail cantonnant des élèves dans des tâches sans garantie d’un gain de compétences.
A l’inverse, la coopération s’entend comme le fait d’agir avec d’autres : cela ne passe pas nécessairement par la réalisation d’un projet commun mais par un besoin individuel. Elle se manifeste par des interactions intentionnelles dans lesquelles les participants tirent un bénéfice de la rencontre (pas forcément le même). [3]
2. Mettre en place une coopération structurée
Le rôle de l’enseignant est essentiel pour préparer les élèves à coopérer. Car, si certaines formes de coopération sont spontanées, la coopération ne va pas de soi, elle s’apprend pour être efficace. Elle doit s’entendre comme un apprentissage (savoir coopérer) au service des apprentissages.
Il s’agit alors pour l’enseignant de:
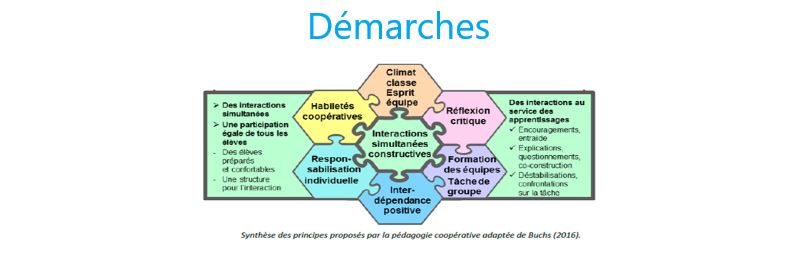
- Définir et d’expliciter les habilités coopératives ( gestion du groupe, fonctionnement du groupe, réflexion, conceptualisation)[4]
- Définir les groupes (2 à 5 maximum) et d’organiser le travail en équipe de manière à favoriser des interactions constructives au service des apprentissages en s’appuyant sur une réflexion critique.
- Définir la tâche à accomplir. L’enseignant doit rendre les apprentissages individuels visibles et la contribution de tous possible et nécessaire afin de développer le sentiment d’interdépendance. Pour cela, S. Connac propose de laisser le choix à l’élève. Si il y arrive seul, tant mieux, c’est intéressant pour lui et pour la classe. Si il demande de l’aide, évoquer avec lui l’intérêt de la coopération. Ce sentiment d’interdépendance positive valorise les élèves dans leur responsabilité individuelle.
- Définir un objectif commun d’apprentissage de tous les élèves : que chaque membre comprenne, apprenne, dépasse un critère prédéfini, progresse dans un climat de classe solidaire.
3. La coopération en mathématiques
Les six compétences mathématiques à acquérir – chercher, modéliser, représenter, calculer, raisonner et communiquer- sont par essence une invitation à la pédagogie coopérative.
Sa pratique est d’ailleurs souvent associée aux activités de résolution de problèmes de recherche mais elle peut être faite dans tous les domaines mathématiques.
Pour preuve, en 2015, une étude[5] a été réalisée sur 108 élèves d’une classe de CM2 sur l’apprentissage des fractions réalisé de manière coopérative en triades hétérogènes (un élève faible, un élève moyen, un élève fort). L’objectif de cette étude était de tester si un travail de groupe coopératif fortement structuré permettait d’améliorer l’apprentissage des élèves, en particulier de niveau moyen dans ces groupes hétérogènes.
Dans la condition faiblement structurée, les élèves devaient faire les exercices en s’organisant comme ils le souhaitaient. Dans la condition fortement structurée, chaque élève s’entraînait pour devenir expert pour l’un des exercices avant de travailler dans sa triade. Lors du travail en triade, à tour de rôle ils étaient responsables de l’une des règles mathématiques et d’une des responsabilités sociales de manière à renforcer la responsabilité individuelle et l’interdépendance positive.
Les résultats montrent que le travail coopératif fortement structuré favorise la compréhension de l’exercice (compétence spécifique travaillée), en particulier pour les élèves de niveau moyen. De plus, une séance de travail coopératif a permis à tous les élèves de progresser (performances mathématiques générales) entre le post et le pré-test.
[1] Définition du CNRTL
[2] Sabourin et Lehraus (2008)
[3] Sylvain Connac, cahiers pédagogiques décembre 2021
[4] Johnson & Johnson 1998
[5] Buchs, Wiederkehr, Filippou, Sommet, & Darnon, 2015