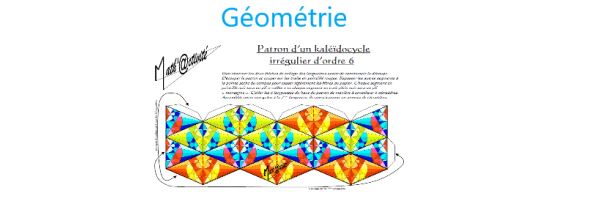
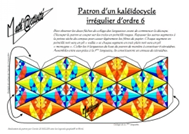
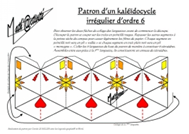
Parce qu’ils sont « curieux, intrigants, beaux, rigolos, ludiques, infinis, géométriques, étoilés, intéressants, spéciaux » (C. Le Beller, professeure de mathématiques à Rennes, APMEP et IREM de Rennes), nous vous proposons de découvrir cette période les kaléïdocycles.
- Définition et historique
Kaléïdocycle” vient du grec. kalos : beau, eidos : aspect, et kuklos : cercle.
Un “kaléïdocycle d’ordre 6” est un anneau de 6 tétraèdres ayant pour faces des triangles (équilatéraux lorsque le kaléïdocycle est régulier et isocèles lorsqu’il est irrégulier). Lorsqu’on le manipule, l’anneau subit une rotation de 180° sur lui-même. Cette rotation “retourne” chaque tétraèdre mais conserve l’anneau dans son ensemble. Ce kaléïdocycle laisse apparaître 4 “faces” différentes constituées chacune de 3 losanges composés de deux triangles isocèles chacun (une face de chaque tétraèdre, soient 6 triangles). Ces faces sont agencées d’une autre façon lorsqu’on retourne le kaléïdocycle.
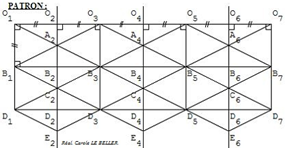
Le modèle de kaléïdocycle d’ordre 6 irrégulier est construit, entre autres, à partir de rectangles dit “rectangles barlongs” (adj. Lat. bis, deux fois, et long) c’est-à-dire composé de deux carrés accolés identiques. Ce rectangle permet de tracer le rectangle d’or et de déterminer le nombre d’or phi, la divine proportion (avec phi = 1,618 034). Ce tracé détermine aussi les éléments de la « quine » des bâtisseurs romans (la paume et la palme en fonction du pied). L’angle aigu en le sommet principal de chaque triangle isocèle est d’environ 53,13°, angle ayant un lien avec le nombre d’or. (cf. livre : La géométrie du nombre d’or de Robert Vincent – Chalagram Edition, 3ème édition, mars 2001).
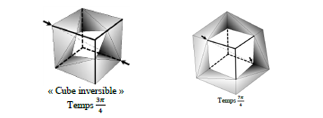
En 1929, Paul Schatz (mathématicien, sculpteur et inventeur allemand) découvre que les solides de Platon peuvent être inversés dont le cube inversible. Ce cube inversible n’est autre qu’un kaléïdocycle particulier (résultat d’un kaléïdocycle d’ordre 6 irrégulier fermé d’ordre 6, coupé tour à tour sur ses 2 plans de symétrie).
En 1958, Wallace Walker (étudiant américain) découvre une grille appelée « forme IsoAxis » qui, une fois pliée, étirée, tordue, déformée, assemblée à une autre et modifiée, devient le développement d’une forme en 3D : un kaléïdocycle.
En 2003, dans son livre « les Kaléïdocycles de M.C. Escher », Marcus Engel énonce les propriétés mathématiques des tétraèdres les composant. Peu de temps après, Rémi Belloeil, professeur de mathématiques, constate que les enveloppes de correspondance traditionnelles permettent de construire simplement des kaléïdocycles irréguliers fermés.
2. Kaléïdocycles et apprentissages géométriques
Il existe différents types de kaléïdocycles irréguliers fermés d’ordre 6, 8, 10, 12, 20, composés de 6,8,10, 12, 20 tétraèdres identiques dont les faces sont des triangles isocèles identiques.
Exemple de kaléïdocycle d’ordre 8 :

De nombreux savoirs et savoir-faire mathématiques peuvent être développés à travers l’étude et la construction de kaléïdocycles avec les élèves :
Au cycle 1, la découverte de cet objet mathématique curieux et intrigant peut être l’occasion de développer des compétences langagières ;
Au cycle 2, les élèves peuvent s’interroger sur comment le reproduire, le construire, ce qui peut favoriser l’observation, la coopération, la connaissance de certaines propriétés géométriques (propriétés du rectangle et du losange, carré, quadrilatère, …) et le réinvestissement du vocabulaire spécifique.
Aux cycle 3 et 4, un travail de construction de cet objet kaléïdocycle qui sort des représentations usuelles peut contribuer à développer des compétences attendues pour ces cycles tout en liant arts, géométrie et langage spécifique (médiatrice d’un segment, diagonales et centre d’un rectangle, triangle isocèle en un sommet, point d’intersection entre deux droites, symétrie axiale, tétraèdre,…).
3. Comment le fabriquer ?
En utilisant le matériel de géométrie suivant : règle, équerre et compas, une feuille A4, de la colle, des ciseaux, un crayon à papier et des crayons de couleurs, il existe un programme de construction qui permet de construire un kaléidocycle irrégulier d’ordre 6. http://mathactivite.free.fr/menus/01p03-kaleidocycle-6.php
De nombreux patrons de kaléidocycles déjà décorés peuvent aussi être téléchargés.
Mais, rien de tel que de les construire et de les décorer soi-même à partir du patron du kaléïdocycle irrégulier d’ordre 6.
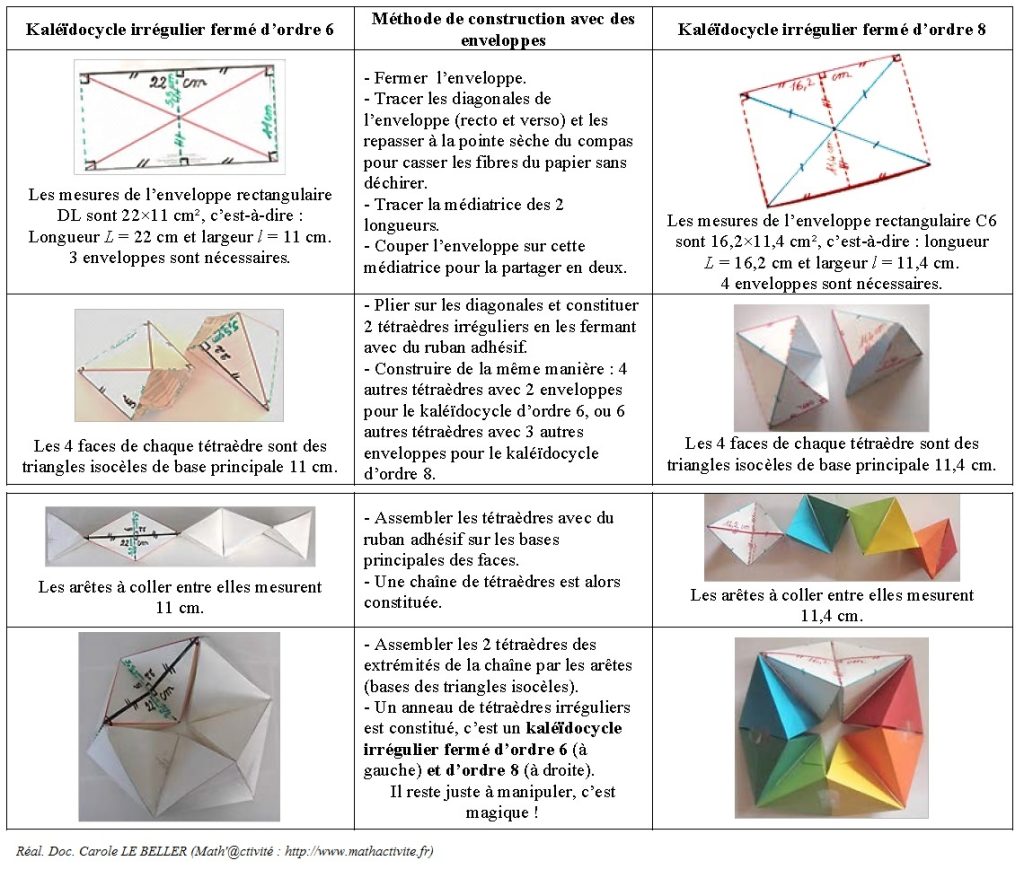
La méthode des enveloppes permet de construire facilement des kaléïdocycles irréguliers fermés d’ordre 6 ou 8.
Enfin, des logiciels de géométrie dynamique 2D et 3D (exemples : Geogebra, Cabri) peuvent aider à la construction de patrons de kaléïdocycles.