L’enseignement de la géométrie à l’école primaire repose sur l’idée d’apprendre à modéliser l’espace. L’intitulé des programmes le stipule expressément : « espace et géométrie ». L’enjeu de l’école est alors bien de renforcer l’acquisition des connaissances spatiales proprement dites tout en amenant les élèves à établir les rapports adéquats entre l’espace et les concepts géométriques qui leur sont enseignés, pour mieux en comprendre la réalité[1]. Le recours à des objets 3D peut être un moyen d’établir ses rapports.
1/ L’enseignement de la géométrie s’appuie sur deux niveaux de connaissance : spatiale et géométrique.
Les connaissances spatiales concernent l’espace sensible, en particulier tous les objets sociaux et professionnels. Elles permettent à l’enfant de maîtriser ses rapports usuels avec cet espace, rapports contrôlés par la perception. Liées à l’expérience, elles s’acquièrent à l’école depuis la maternelle mais aussi en dehors de tout enseignement (repérage, positions relatives d’objets, parcours, association d’objet et donc leur fabrication…).
La géométrie émerge du rapport au sensible : l’étude et la classification d’objets du monde sensible et la rencontre d’objets géométriques par la perception et la manipulation.
Les connaissances géométriques portent sur des objets théoriques 3D et/ou 2D (objets idéaux), mais qui ont des représentations dans l’environnement familier des élèves. Ces objets peuvent être à terme définis par un texte (cube, tétraèdre, carré, segment…) ou non (points, droites…) et par leurs relations (parallélisme, perpendicularité, distance…).
La géométrie entretient donc des liens complexes avec l’espace physique qui nous entoure : elle élabore hors de l’expérience sensible des concepts, des relations que le sensible permet de rendre tangible.
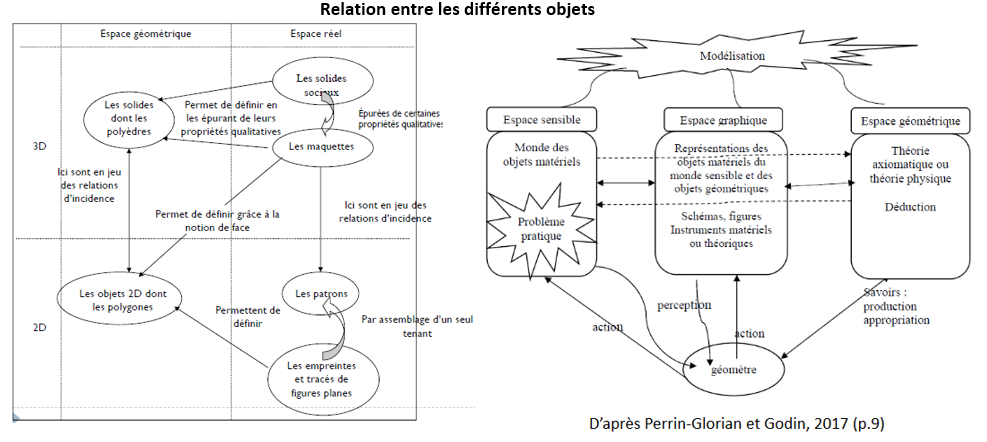
Ce double aspect est présent dans la géométrie enseignée au cycle 3 : les élèves peuvent élaborer ou utiliser des modélisations de situations spatiales à l’aide de dessins ou de tracés, cette modélisation pouvant ou non s’appuyer sur des relations géométriques.
2 /Difficultés rencontrées par les élèves[2]
La représentation des objets de l’espace s’opère par le passage de l’espace au plan ; celui-ci constitue une perte considérable d’informations et est source d’erreurs.
- Les erreurs liées à la reconnaissance du solide : s’il n’y a pas appropriation des conventions de représentation en perspective, l’élève peut percevoir la représentation du cube comme une figure composée d’un carré juxtaposé de deux parallélogrammes. Les propriétés liées à ce solide ne lui apparaissent pas. L’image mentale de l’objet se construira alors difficilement et ne permettra pas à l’élève de reconnaître les différents patrons d’un solide sans reconstitution effective de celui-ci.
- Les erreurs liées au vocabulaire : les élèves utilisent le vocabulaire lié à la géométrie plane pour désigner des objets de l’espace (« figure » à la place de « solide », « carré » à la place de « cube ») et ils confondent très souvent les mots « arêtes » et « cotés » qui désignent un même objet, nommé différemment selon qu’il est situé dans une figure plane ou un solide.
- Les erreurs liées à la représentation : un conflit surgit entre ce que l’on sait et ce que l’on peut représenter par le dessin, ou entre ce que l’on voit et ce que l’on cherche à savoir par la représentation.
Bernard Parzysz[3] explique que la « représentation que l’élève fait d’un objet de l’espace est le résultat d’un compromis entre ce qu’il sait (le su) et ce qu’il voit ou plutôt la représentation qu’il a de l’objet (le vu). Il est amené à opérer des choix, c’est à dire à éliminer de la représentation certains aspects du voir et certains aspects du savoir. » Ex :« Dans la perspective cavalière d’un cube par exemple, l’élève essaie de représenter tous les angles droits et oublie de représenter les arêtes cachées ».
- Les erreurs liées à l’enseignement reçu : l’enseignement de la géométrie des solides se fait souvent à partir de représentations des solides (manuels, fiches photocopiées, …). Il s’appuie essentiellement sur la désignation du vocabulaire spécifique aux polyèdres (faces, arêtes et sommets) que les élèves devront apprendre, sans manipuler les solides dans des activités porteuses de sens. Afin de permettre à ceux-ci de faire le lien entre les objets et leurs représentations diverses, il est important de mettre des solides pleins ou évidés, à leur disposition.
3/ Un des enjeux de la géométrie à l’école : passer progressivement d’une géométrie perceptive à une géométrie instrumentée puis déductive.
Pour établir cette bascule progressive, l’élève doit être capable de développer sa capacité à articuler des visions 3D, 2D, 1D et 0D[4].
La géométrie dans l’espace est le point de départ des activités géométriques à l’école primaire. Dès la petite section, les élèves sont capables d’une observation fine d’objets géométriques tridimensionnels.
Partir d’objets de la vie courante se révèle alors beaucoup plus facile. En effet, leur perception globale fournit des informations sans ambiguïté par rapport aux propriétés géométriques que l’on veut faire acquérir. Proposer aux élèves des objets matériels suffisamment nombreux et variés leur permettra de se constituer un champ d’expériences sur lesquels ils pourront progressivement construire les concepts géométriques mentionnés dans les programmes.
La maîtrise des compétences liées à la géométrie dans l’espace (limitée à l’étude des solides) se fera par des situations qui devront faire travailler l’articulation entre « l’objet de l’espace » et ses différentes représentations. Les élèves pourront se construire des images mentales et pourront alors abandonner la manipulation systématique de ces objets pour comprendre les activités proposées au collège. Le travail de construction ou de reproduction de solides est guidé par un enjeu de déconstruction et reconstruction dimensionnelle reposant sur la mise en relation de sous-unités de différentes dimensions.
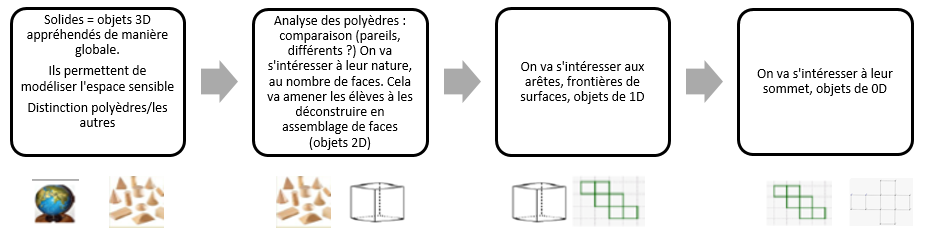
Permettre aux élèves d’agir en mathématiques, c’est aménager par les enseignements un passage progressif de la manipulation à l’expérimentation. En permettant aux élèves de dépasser le hasard du tâtonnement au profit de l’action orientée vers un but, on problématise les situations d’apprentissage. Lors d’une expérience, les gestes provoqués sont guidés par une intention, une organisation, ainsi que par le raisonnement.
[1] Article Grand N n°53 René Berthelot et Marie-Hélène Salin, 2019
[2] « La galerie des polyèdres », groupe maths Académie de Créteil
[3] Docteur en sciences et techniques communes (Paris 7, 1989). – Maître de conférences à l’IUFM de Lorraine et à l’université de Metz (en 1999), fait partie de l’apmep
[4] « Enseigner la géométrie élémentaire – Enjeux, ruptures et continuités », Anne-Cécile Mathé, Thomas Barrier, Marie-Jeanne Perrin-Glorian
