« Les grandeurs demeurent sans doute un passage obligé pour les enfants. D’abord, nous vivons au milieu d’objets qu’il nous faut, avant toute idée élaborée de mesure, saisir sous l’aspect de grandeurs (…). Ensuite, puisqu’on recourt sans cesse à des mesures dans la vie civilisée d’aujourd’hui, il faut bien apprendre en quoi elles consistent et ce qu’elles nous apportent (…) » (Friedelmeyer, Irem de Strasbourg, 2001)
La question des grandeurs et de la mesure est abordée à l’école dès le plus jeune âge (cycle 1, cycle 2, cycle 3) et fait l’objet d’un domaine spécifique car elle est un des points de départ des mathématiques mais aussi de la physique. Son enseignement a pour objectif de permettre aux élèves de comprendre le sens des mesures de grandeurs qu’ils rencontrent à l’école ou dans leur vie quotidienne et qu’ils rencontreront dans un cadre professionnel.
Il repose sur trois étapes progressives fondamentales qui permettent de passer de la grandeur perçue à la grandeur mesurée:
- Donner du sens à la grandeur
- Donner du sens à la mesure
- Mesurer
- Donner du sens à la grandeur
La grandeur peut se définircomme un concept qui permet de décrire les objets ou les phénomènes.
L’appréhension de ce concept pour un objet ne peut se faire qu’en comparaison avec un autre objet.
La construction du sens de la grandeur, indépendamment de la mesure, se fait par le biais de :
- l’estimation visuelle ou kinesthésique
- la comparaison directe : juxtaposition, superposition, mise en regard de deux objets ;
- la comparaison indirecte : recours à un objet intermédiaire, à un instrument de report ou transformation de l’un des objets pour le rendre comparable à l’autre.
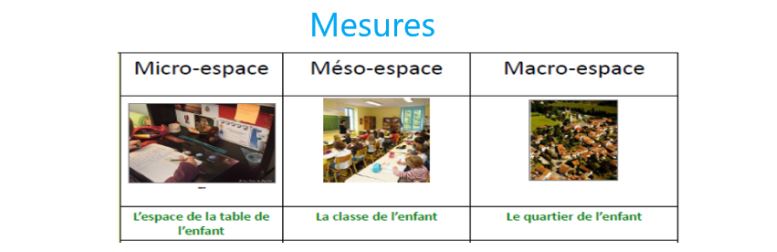
Selon J.L Bregeon, professeur de mathématiques à l’IUFM d’Auvergne, les scenarios d’apprentissage doivent aussi être pensés dans les différents espaces géométriques.
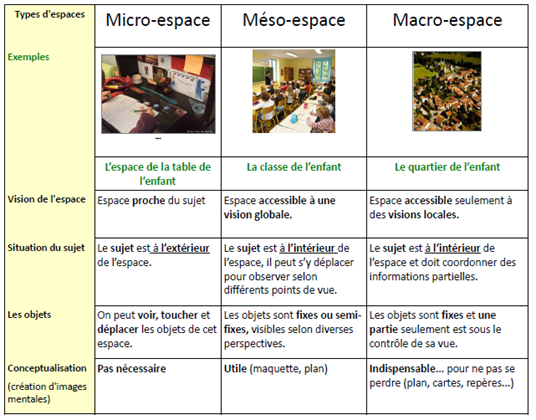
Ainsi, les élèves arrivent mieux à conceptualiser chaque grandeur.
L’importance de cette conceptualisation avant la mesure est soulignée par de nombreux chercheurs. Dans sa thèse, pour le cas de la grandeur masse, D. Passelaigue, professeur d’Université de Montpellier (2011) a montré que les activités de comparaison sont une aide à la conceptualisation : notamment les élèves ayant vécu une situation de comparaison différencient mieux la masse du volume que ceux qui entrent directement dans des activités de mesurage à l’aide d’un instrument du quotidien affichant la référence conventionnelle (le gramme).
Pour comprendre ce qu’est une grandeur, il est aussi important de distinguer deux types de grandeurs :
- la grandeur mesurable : grandeur à laquelle on peut affecter une valeur numérique à partir d’observations. En outre, la somme et/ou le produit de grandeurs mesurables a une signification. Parmi les grandeurs mesurables, on peut citer la longueur, la masse, le temps…
- la grandeur repérable : elle est dite repérable si la somme et le produit de cette grandeur n’ont pas de sens. Parmi les grandeurs repérables, on peut citer la température centésimale (°C), la date, le potentiel électrique…
2. Donner du sens à la mesure
La mesure se définit comme « l’évaluation d’une grandeur par comparaison avec une grandeur de même espèce prise comme référence (unité, étalon) » (Malifaud, 2008) ou encore comme « le rapport de cette grandeur à une autre grandeur de même espèce choisie comme unité » (De Broglie, 1955).
Construire le sens de la mesure, c’est passer progressivement d’étalon arbitraire à des étalons référents avec la mise en évidence du besoin de ces étalons référents (unité usuelle ou légale).
C’est aussi avoir recours à des outils simples puis à des outils conventionnels.
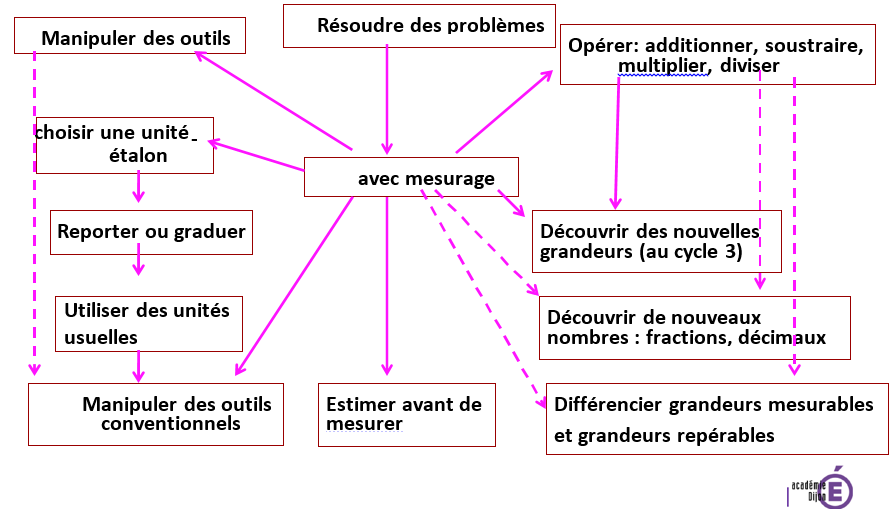
3. Mesurer
C’est le dernier stade avec l’incursion du nombre et les rapports entre les différentes unités.
Il s’agit alors de :
- de s’interroger sur l’adaptabilité de l’unité usuelle à la grandeur mesurée
- d’étudier les relations entre les différentes unités
- d’effectuer des calculs.