M@ths en vie, une démarche qui facilite le passage de la représentation à la modélisation
Représenter
- Donner à voir (premier niveau de représentation commun entre autres aux mathématiques et à d’autres disciplines)
- Mettre en évidence des relations entre les objets (ex. codage géométrique)
- Représenter des objets abstraits, qui n’ont pas d’autre mode d’existence que cette représentation : des nombres décimaux, des fractions, en un mot des objets mathématiques, qui est un troisième niveau de représentation et qui est le moins intuitifs pour les élèves car les objets ne sont pas accessibles en eux-mêmes, seulement par leurs représentations.
Ces représentations diverses peuvent appartenir à différents registres : registre graphique, registre du langage naturel (« un parallélépipède à 6 faces »), registre numérique, registre de l’écriture symbolique https://cache.media.eduscol.education.fr/file/Competences_travaillees/20/7/RA16_C4_MATH_representer_N.D_566207.pdf (document EDUSCOL)
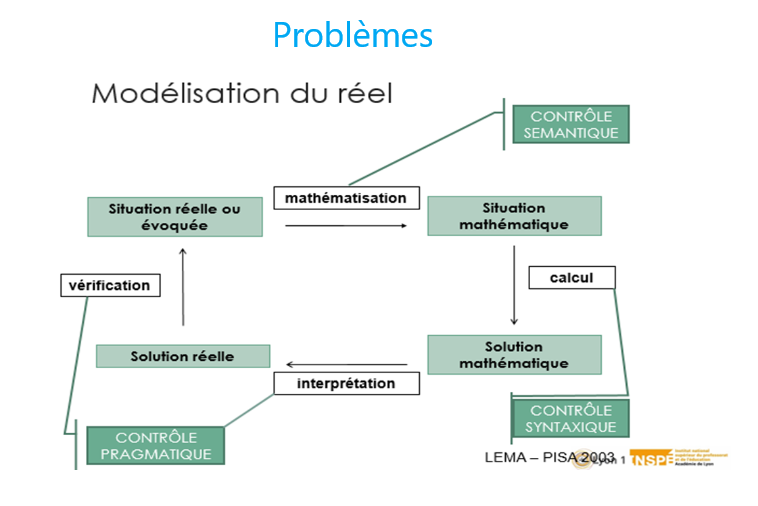
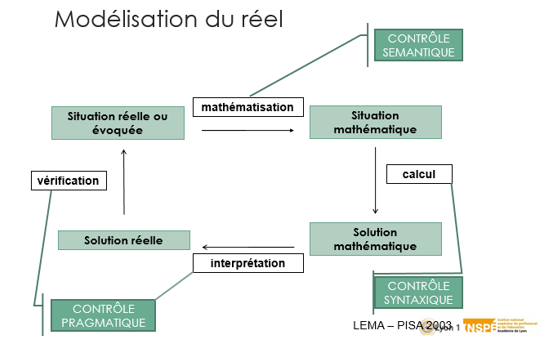
Modéliser : Traduire en langage mathématique une situation réelle
https://cache.media.eduscol.education.fr/file/Competences_travaillees/17/7/RA16_C4_MATH_modeliser_N.D_566177.pdf (document EDUSCOL)
⇒ Trois temps : la mise au point d’un modèle à partir du réel, le fonctionnement du modèle lui-même à l’intérieur des mathématiques, et la confrontation des résultats du modèle au réel.
En exerçant les élèves à repérer des situations réelles pouvant faire l’objet d’un investissement mathématique, ils se créent un répertoire de représentations qu’ils pourront ensuite mobiliser dans d’autres situations similaires.
L’utilisation de la photo permet de construire ce temps intermédiaire entre une situation vécue, réelle et une abstraction abstraite visée par l’exercice scolaire.
Alain Descaves, IREM (Institut de recherche sur l’enseignement des mathématiques) propose de mettre en relation « différents systèmes de représentation (langue naturelle, représentations iconiques, matériels, écrits mathématiques), source d’enrichissement du sens, Cette mise en correspondance permet alors d’aider à la compréhension de l’énoncé. L’utilisation de systèmes matériels de représentation (iconiques, symboliques, etc.) facilite le passage de la représentation du problème à celle de la solution.
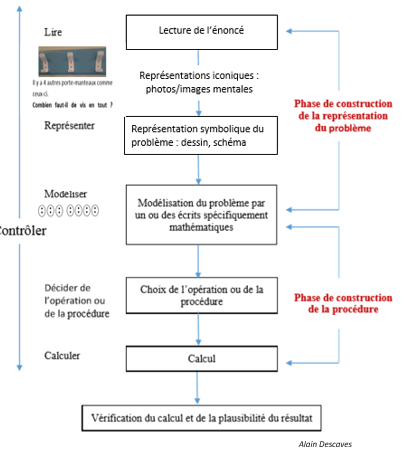
L’utilisation de la photo permet d’alléger la tâche « s’approprier le problème ». Elle est une aide à la représentation du problème et peut faciliter le passage à la modélisation.