Beaucoup d’instruments sont très souvent mis à disposition des élèves : des instruments classiques (règle, équerre, compas, …), en 2D (gabarits, pochoirs, papier quadrillé, pointé, percé), à dimension « exotique » (règle muette, ficelle tendue, …) et des objets quotidiens. Mais l’usage des instruments usuels de géométrie par les élèves nécessite une certaine instrumentation (Rabardel, 1995), c’est-à-dire la construction par les élèves de schèmes gouvernant l’usage de ces instruments.
Le mot du chercheur de ce mois vous propose de réfléchir à la place des instruments en géométrie dans les programmes, leur rôle et le « coût » qu’on peut leur donner selon les objectifs visés.
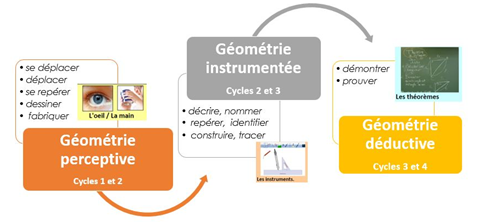
- Les instruments dans les programmes et éléments de progressivité
Au cycle 1, dans le domaine « Explorer des formes, des grandeurs, des suites organisées », sans pour autant parler d’instruments, l’approche des formes planes, des objets de l’espace, des grandeurs, se fait par la manipulation et la coordination d’actions sur des objets. Les élèves utilisent ou produisent diverses représentations de l’espace à trois dimensions (photos, maquettes, dessins, plans…). Cette approche est soutenue par le langage : il permet de décrire ces objets et ces actions et favorise l’identification de premières caractéristiques descriptives. Ces connaissances constituent une première approche de la géométrie et de la mesure qui seront enseignées par la suite.
Au cycle 2, la reproduction de figures diverses, simples et composées est une source importante de problèmes de géométrie dont on peut faire varier la difficulté en fonction des figures à reproduire et des instruments disponibles. Il est attendu des élèves de savoir utiliser la règle, le compas ou l’équerre comme instruments de tracé. Il est aussi attendu de faire le lien entre propriétés géométriques et instruments de tracé : droite, alignement et règle non graduée ; angle droit et équerre ; cercle et compas.
Prolongeant le travail amorcé au cycle 2, les activités au cycle 3 permettent aux élèves de passer progressivement d’une géométrie où les objets (le carré, la droite, le cube, etc.) et leurs propriétés sont essentiellement contrôlés par la perception à une géométrie où le recours à des instruments devient déterminant, pour aller ensuite vers une géométrie dont la validation s’appuie sur le raisonnement et l’argumentation. L’utilisation fréquente des outils de construction permet de renforcer la compréhension des propriétés étudiées (perpendicularité, égalité de longueurs, parallélisme, milieu, symétrie, égalité d’angles, etc.) et constitue un enjeu majeur de l’enseignement de la géométrie. RA16_C3_MATH_Espace-geometrie_897385.pdf
2. Le rôle des instruments en géométrie
Les instruments constituent une variable didactique majeure pour l’enseignement de la géométrie. Ne pas hésiter à varier les instruments, mais ne pas négliger le temps de prise en main. De nombreux rôles peuvent leur être attribués (Mithalal- Le Doze- 2019) :
– Pallier les limites de la visualisation dans les cas d’incertitude, et affiner les concepts construits.
– Matérialiser des propriétés géométriques : les découvrir, associées à un instrument ; matérialiser des propriétés connues.
– Porter l’attention sur des caractéristiques spécifiques des objets.
– Porter l’attention sur l’identification de constituants des objets et leurs relations (les propriétés).
– Soutenir l’analyse des dessins en ajoutant des tracés supplémentaires.
Les instruments sont utilisés pour guider, outiller la perception, et leur usage nécessite la mise en œuvre de propriétés géométriques. Il doit donc y avoir une nécessaire interaction entre connaissance des propriétés géométriques et utilisation des instruments de géométrie. 77n2.pdf
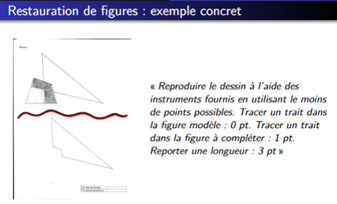
Exemples : le rectangle à terminer
Les stratégies vont être complètement différentes selon l’instrument utilisé pour terminer ce rectangle.

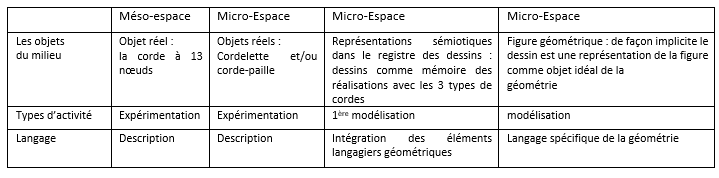
Selon l’instrument choisi, on favorise aussi l’espace dans lequel on va travailler. Ainsi, dans le cas de la corde à 13 nœuds, on préfère dans un premier temps l’activité dans un monde réel (le méso-espace) pour arriver à l’objet géométrique (micro espace). Ce passage du monde réel au cadre géométrique s’accompagne d’une transformation conceptuelle qui va de pair avec une évolution du langage dans un processus de secondarisation des genres (Rebière, 2002, 2013). Ainsi, la situation dans le méso-espace utilisant la grande corde suscitera vraisemblablement un langage renvoyant au milieu matériel objectif : corde, nœud, intervalle, écart, tenir un nœud avec une main, tendre la corde entre le premier nœud et le quatrième nœud, etc. Le passage au dessin pour garder la mémoire de la pré-figure devrait faire évoluer ce discours vers les formulations suivantes : pointe, point, sommet, trait droit, côté, forme, triangle, quadrilatère, rectangle, etc. Une dernière étape du processus sera de parvenir à dégager et institutionnaliser un objet géométrique dont les caractéristiques appartiennent au cadre géométrique avec les termes spécifiques : point, sommet, segment, côté, milieu, triangle, quadrilatère, longueur, etc… Cette transformation conceptuelle et langagière s’inscrit dans une première phase d’un processus de modélisation, ce qui reprend l’une des fonctions de la géométrie soulignée par Brousseau.
3. L’introduction des « coûts » des instruments
Et si au lieu d’imposer des instruments aux élèves, on leur donnait un coût ?
Pour Duval, Godin (2005) « ce n’est pas tant la tâche de reproduction qui est importante que le type d’instrument choisi pour la reproduction » car selon l’instrument choisi, on sollicite telle ou telle vision.
L’introduction d’un coût à l’utilisation des instruments permet la réussite par des procédures diverses, qui demandent plus ou moins de connaissances géométriques, mais incite à utiliser certains instruments plutôt que d’autres.
Sans contraindre les instruments, on peut favoriser l’usage de ceux qui mènent aux procédures que l’on veut développer par un jeu de malus. Un enjeu transverse à travailler dès le cycle 2 : articulation entre déconstruction instrumentale (opératoire) et dimensionnelle (en lien avec un référentiel théorique).
Exemples :