Page 9 of 11
Ce nâest pas parce que lâĂ©lĂšve joue quâil apprend. Tout dĂ©pendrait des temps de « dĂ©briefing » qui aideraient Ă conscientiser les savoirs en jeu.
Une fiche de préparation et des documents clés en main pour utiliser le Boggle Maths en classe pour tous les cycles.
Une mallette de ressources et dâactivitĂ©s Ă destination des enseignants, des formateurs et des Ă©lĂšves : une focale sur la gĂ©omĂ©trie.
Le tryptique MVA en géométrie
– Les enjeux des activitĂ©s de manipulation
– Le rĂŽle du langage dans lâenseignement de la gĂ©omĂ©trie
Des activités pour tous les cycles et facilement intégrables à votre programmation en géométrie.
Une ressource pour unifier les modélisations et simplifier les représentations : quels avantages ? Comment construire ces schémas en barre ?
Faire un schĂ©ma, ça sâapprend ! Un apprentissage explicite pour construire des savoirs.
Des éléments de progressivité pour une installation du schéma en barre.
– Au cycle 1 : utilisation des rĂ©glettes Cuisenaire ou des lĂ©gos.
– Au cycle 2 : un exemple en CE1 facilement transposable.
– Au cycle 3 : des exemples de schĂ©matisations avec des problĂšmes impliquant des fractions.
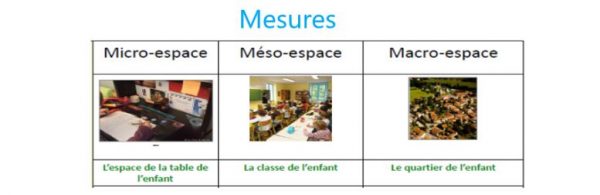
La matrice dâapprentissage en grandeurs et mesures proposĂ©e par lâacadĂ©mie de Martinique fixe les composantes incontournables pour Ă©laborer une progression de cycle et dâĂ©cole.
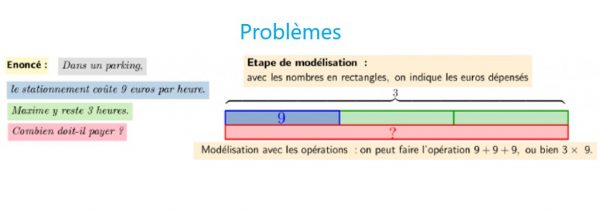
3 étapes progressives qui permettent de passer de la grandeur perçue à la grandeur mesurée : donner du sens à la grandeur, à la mesure et mesurer.